本篇目录:
旋转型相似三角形(经典)
1、全等三角形共有5种判定方式:SSS、SAS、ASA、AAS、HL。特殊情况下平移、旋转、对折也会构成全等三角形。SSS(边边边),即三边对应相等的两个三角形全等。
2、八种:A字型和倒A字型,8字型,母子型,一线三等角,混合型,旋转型,双垂型和共享型。相似三角形是几何中重要的证明模型之一,是全等三角形的推广。全等三角形可以被理解为相似比为1的相似三角形。
3、相似三角形:相似三角形有平行线型(带平行线的相似三角形),相交线型,旋转型。当出现相比线段重叠在一直线上时(中点可看成比为1)可添加平行线得平行线型相似三角形。
4、SAS相似定理(边-角-边相似定理):如果两个三角形的一个角相等,两个对应边的比例相等,那么它们是相似的。如果两个对应边的比例相等,而另外一个对应边也相等,那么这两个三角形是全等的。
5、相似三角形面积的比等于相似比的平方。相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是相似比的平方。
6、设腰长a,底边长b。有两种可能:5a=6,或者5a=15 当5a=6时:a=4,于是底边长15-a/2=13 此时132a,根据“三角形两边之和大于第三边”可知,该情况不成立。
初中数学题——旋转型相似
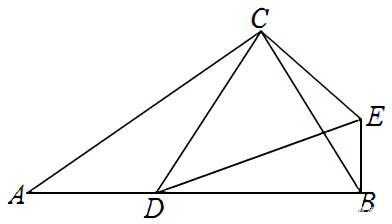
旋转型相似三角形—相似三角形基本图形专题复习A12ECBD绍兴市柯桥区马鞍镇中学周峰AD如图,在ΔABC中,∠ADE=∠B,则图中相似的三角形是。
有两种可能:5a=6,或者5a=15 当5a=6时:a=4,于是底边长15-a/2=13 此时132a,根据“三角形两边之和大于第三边”可知,该情况不成立。当5a=15时,a=10 底边长6-a/2=1,成立。
初中数学旋转题型口诀如下:遇到旋转找关键点,连接对应点,基本性质记心间。旋转的性质是很多考生在答题时的痛点,很多考生面对旋转问题往往束手无策。
一,旋转型——题目中的图形需要顺时针或逆时针旋转,平面旋转和立体旋转,不同角度的旋转。二,对称型的——观察图形是否为对称图形或中心对称。三,字母形的和汉字型——观察其笔画数目或相邻字母相隔的字母数。

相似三角形有平行线型(带平行线的相似三角形),相交线型,旋转型;当出现相比线段重叠在一直线上时(中点可看成比为1)可添加平行线得平行线型相似三角形。
解析旋转开关结构特点及工作原理
旋转开关是以旋转手柄来控制主触点通断的一种开关。旋转开关的结构形式也有两种,分别是单极单位结构和多极多位结构。单极单位旋转开关在应用中常与转轴式电位器共同使用,而多极多位旋转开关多用于工作状态线路的切换。
旋转开关结构特点 旋转开关的结构有两种,一种是MBB接点型,另一种是BBM接点型。第一种的特点是在换位的时候动接点与前后的接点都是接触的,然后它会断开前接点,保持与后接点的接触。
旋转开关的结构形式单极单位和多级单位结构,单极单位结构都是与转轴式的电器一起使用,多级单位旋转开关大部分都是用在线路切换式的地方。
初二相似图形(旋转类)例题!
1、ACBBC“旋转型”相似三角形的应用如图,在ΔABC中,AB=AC,D为线段AB上一点,作ΔEDC∽ΔABC,连接AE,求证:AE//BC。
2、有两种可能:5a=6,或者5a=15 当5a=6时:a=4,于是底边长15-a/2=13 此时132a,根据“三角形两边之和大于第三边”可知,该情况不成立。当5a=15时,a=10 底边长6-a/2=1,成立。
3、丶重叠部分的DEF面积显然与DEF的边长有关。假定DEF的直角边也为1,则重叠部分为一个对角线长为根号2/2的正方形,面积为1/4。
4、所以得方程a/b=b/(a-b)化简a*a-ab=b*b 变形(a-b/2)*(a-b/2)=b*b+b*b/4 解得a=(1+根号5)*b/2 所以答案是(1+根号5)*/2 和第一题类似,不过很容易。
5、因此BG=DE,设DE与CG、BG的交点分别为O、M,因为两个三角形全等,所以角CED=角CGB,又因角EOC=角GOM,所以俩三角形为相似三角形,所以角GMO=角GCE=90度,所以BG与DE垂直。
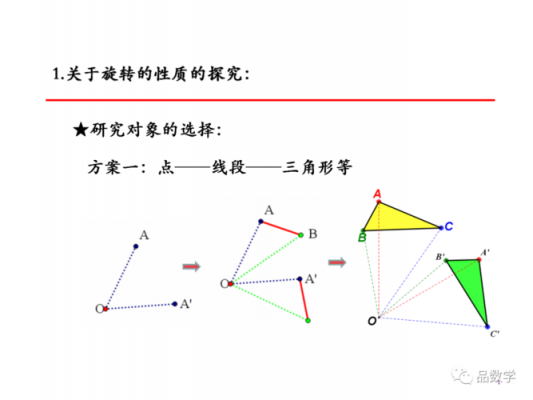
6、A要转到D,B要转到A,转了90度,旋转中心应当是正方形的中心。
到此,以上就是小编对于相似与旋转模型经典例题的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏