本篇目录:
- 1、请问如何证明一个函数是单射,在函数不是单调的情况下,比如1-x/1+x这...
- 2、设f:x-y,g:y-x,设g.f为x上恒等的函数,证明:f是单射,g是满射
- 3、对于函数f:ZxZ-ZxZ,f()=,证明f是单射函数、满射函数.
- 4、如何证明单射满足左消去律?
请问如何证明一个函数是单射,在函数不是单调的情况下,比如1-x/1+x这...
首先函数不都是单射,如f(x)=x,f(-1)=f(1)=1。但是反函数都是单射。函数和它的反函数(如果存在的话)都是单射。因为单射的函数存在反函数。
首先,计算函数在给定区间内的导数。导数表示函数在某一点上的变化率。如果导数在整个区间内都大于零(即导数为正),则函数在该区间上是递增的(单调递增)。这意味着函数的取值随着自变量的增加而增加。
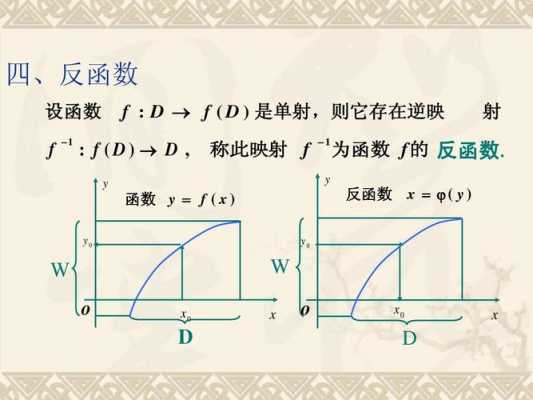
用反证法。假设f不是单射,即有两个X上的不同点的像相同,即存在x1,x2两个不同点,它们都被f映成y。可是g再把y映回来的时候,只能映为x1或者x2或者其他一个什么点,即g。
要判断一个函数在某个区间上的单调性,可以通过导数的正负来进行判断。 首先,计算函数在给定区间内的导数。导数表示函数在某一点上的变化率。
用反证法证明。假设g不是单射,不妨设B中元素a,b由g映射到C中同一元素c上,则因为f是满射,所以存在A中元素d,f分别由f映射到a,b上,所以d,f由f⊙g映射到c上,即f⊙g不为单射。与条件矛盾,假设不成立。
设f:x-y,g:y-x,设g.f为x上恒等的函数,证明:f是单射,g是满射
1、所以F为单射,否则 x1!=x2 y=f(x1)=f(x2)则x1=g(y)=x2 矛盾 G为满射,否则 存在x0 s.t.不存在g(y0)=x0 则与g。f(x0)=x0矛盾(取y0=f(x0))同理 因为F。
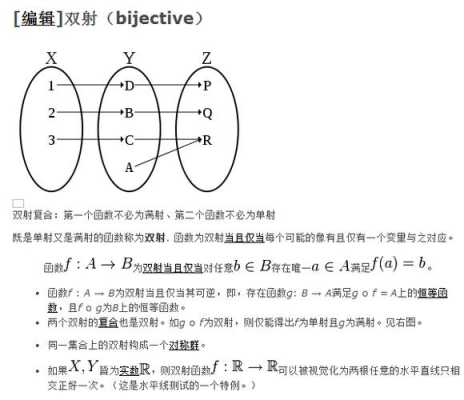
2、假设g不是单射,不妨设B中元素a,b由g映射到C中同一元素c上,则因为f是满射,所以存在A中元素d,f分别由f映射到a,b上,所以d,f由f⊙g映射到c上,即f⊙g不为单射。与条件矛盾,假设不成立。所以g一定为单射。
3、正确的结论是:f是单射,但是g未必是单射。设X={a,b},Y={d,e,f},Z={g,h}。f:a→d,b→e。g:d→g,e→h,f→h。那么g(f(x))):a→g,b→h,是单射。f单,g不单。
4、设函数 y = f(x) = (x+1)^2/2 + 2x + 3。根据链式法则,如果 y = f(u) 和 u = g(x),则 y = f(u) × g(x)。此外,幂函数的导数是 (u^n) = n × u^(n-1)。
5、函数的近代定义是给定一个数集A,假设其中的元素为x,对A中的元素x施加对应法则f,记作f(x),得到另一数集B,假设B中的元素为y,则y与x之间的等量关系可以用y=f(x)表示,函数概念含有三个要素:定义域A、值域B和对应法则f。
6、g(-x)=f(-x)-f(x)=-g(x)因此 g(x) 是奇函数。
对于函数f:ZxZ-ZxZ,f()=,证明f是单射函数、满射函数.
1、设f(a,b)=f(c,d),则a+b=c+d,a-b=c-d,解得a=c,b=d,所以是单射。下面证明是满射 对任意的(a,b),x+y=a,x-y=b,有解 x=(a+b)/2,y=(a-b)/2,即平面内的每一个点都有原像存在。
2、构造从x至ax的单射函数f。由于单射的性质得出若fu=fv,则u=v。将fu与fv替换,则有au=av。所以得出结论:若f是单射且au=av,则u=v。既满足左消去律。设函数f:A-B。
3、单射函数定义:如果函数f从集合A到集合B,且对于集合A中的任意两个元素x1和x2,如果f(x1)=f(x2),则x1=x2,那么函数f是一个单射函数。
4、首先,我们来看待括号中的部分 (2-X^2)^(1/2)。这是一个幂函数,指数是 1/2,表示开平方。我们可以把这个部分看作一个函数 f(x) = (2 - x^2)^(1/2)。
如何证明单射满足左消去律?
可消去是矩阵可逆的充要条件。例如: AB=AC 若A可逆,等式两边同时乘A的逆即可。
假设G为满足条件的半群,g∈G。定义映射:G-G使得(h)=g*h,则由消去律易知是单射(假设(h1)=(h2),即g*h1=g*h2,则h1=h2)。
设A、B是集合,| A |=2,| B |=3,则共可定义 9 个从A到B的映射,其中有 6 个单射,有 0 个满射,有 0 个双射。
步骤是: (1+) 自X取出特别的x和y满足F(x)=F(y) (2+) 证明x≠y。 也就是找出反例,说明单射定义不成立 例:若g o f是单射,g 不一定是单射。 [这问题既非证明 g 是单射,亦非证明 g 不是单射。
若设 的所有中间域 组成集合 ,容易证明 E 对 中的所有元素都是有限伽罗瓦扩张。若设 G 的所有子群构成集合 ,则以上结论则建立了从 到 的单射 ,它满足公式(8)。反之对任何 ,首先有 ,而由公式(6)得 ,所以有 。
向量的数量积与实数运算的主要不同点:向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2。向量的数量积不满足消去律,即:由a·b=a·c(a≠0),推不出b=c。
到此,以上就是小编对于函数为单射的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏