本篇目录:
马尔科夫链和随机是啥关系!什么意思阿?
马尔科夫链的数学背景 马尔可夫链,因安德烈马尔可夫(A.A.Markov,1856-1922)得名,是数学中具有马尔可夫性质的离散时间随机过程。
马尔可夫链指的是已知现在的条件下,过去的信息与未来是独立的,这个独立是条件独立性。
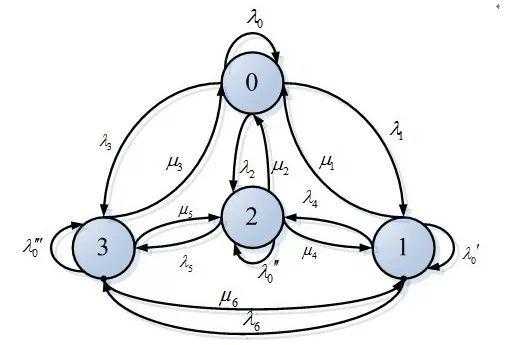
马尔可夫链是满足下面两个假设的一种随机过程:t+l时刻系统状态的概率分布只与t时刻的状态有关,与t时刻以前的状态无关;从t时刻到t+l时刻的状态转移与t的值无关。
马尔可夫链是概率论和数理统计中具有马尔可夫性质且存在于离散的指数集和状态空间内的随机过程 马尔可夫链可通过转移矩阵和转移图定义,除马尔可夫性外,马尔可夫链可能具有不可约性、常返性、周期性和遍历性。
马尔可夫链(Markov Chain),描述了一种状态序列,其每个状态值取决于前面有限个状态。马尔可夫链是具有马尔可夫性质的随机变量的一个数列。
“不可约的马尔可夫链”通俗的讲是什么意思?
马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。
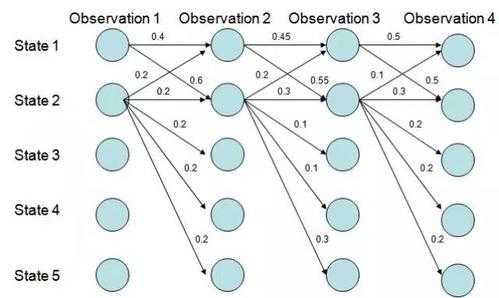
通俗简单的理解马尔科夫链:马尔可夫链指的是已知现在的条件下,过去的信息与未来是独立的,这个独立是条件独立性。
不可约马尔可夫链(irreducibleMarkovchain)一种马尔可夫链。指状态空间E是惟一闭集的马尔可夫链,这又相当于E不含两个不相交的非空闭集。
什么是马尔可夫随机场
马尔可夫链,因安德烈马尔可夫(A.A.Markov,1856-1922)得名,是数学中具有马尔可夫性质的离散时间随机过程。
马尔科夫随机场不属于有限混合模型。马尔科夫随机场属于概率图模型,是典型的马尔可夫网,是一种无向图的生成模型,主要用于定义概率分布函数。所以不属于有限混合模型。
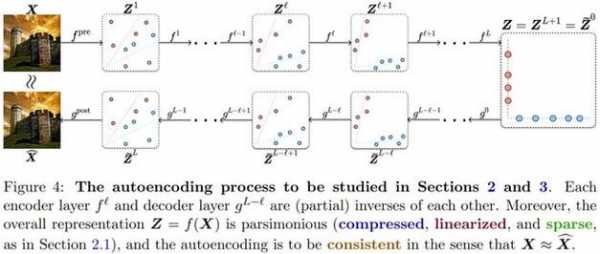
无向图模型,也称为马尔可夫随机场或马尔科夫网络,是一类用无向图来描述一组具有局部马尔可夫性质的随机向量 的联合概率分布的模型。
概率图模型可大致分为两类:一类是有向图模型,表示变量间的依赖关系,也称为贝叶斯网;一类是无向图模型,表示变量间的相关关系,也称为马尔科夫网或马尔科夫随机场。
到此,以上就是小编对于马尔科夫链的初始分布的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏