本篇目录:
- 1、请问泊松积分等于多少啊?
- 2、泊松积分公式的定义是什么?
- 3、什么是“泊松积分”?
- 4、泊松积分是怎么证明的
- 5、求泊松积分公式
- 6、如何求泊松积分?
请问泊松积分等于多少啊?
1、= 2π。所以(-∞到∞)∫e^(-x)dx = √(2π)。所以(-∞到∞)∫e^(-x/2)dx =2 √(π)。这个就是泊松积分,并不是泊松积分的一半,其结果等于π^(1/2)/2,建议直接记结果。
2、et方dt等于√π/2。∫[-∞,+∞]e^tdt=2∫[0,+∞]e^tdt2∫[0,+∞]dt=+∞,所以上面的无穷积分是发散的。

3、这个积分是泊松积分,而泊松积分的值就等于√π的话,这道题目的答案不用计算就知道是√π/2,泊松积分这样的常用积分的值你如果能记住的话,对快速解题很有帮助。
4、泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。泊松积分公式是圆域狄利克雷问题的求解公式。
5、泊松分布是与这种过程相关的一种概率分布,通常用于计算在一定时间或区域内,某一事件发生的概率。泊松分布的参数λ表示单位时间或单位区域内平均发生事件的次数。
泊松积分公式的定义是什么?
1、松积分公式是一个重要的数学公式,用于计算维三维的球面分。它由法国数学家西蒙·泊松于19世纪出。
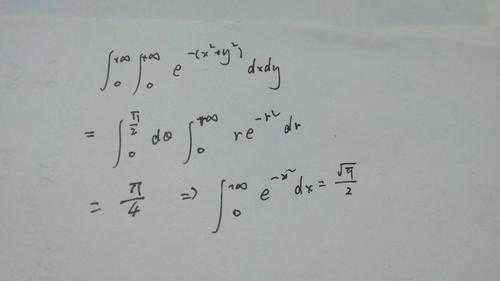
2、泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。
3、泊松公式为:P(k)=(λ^k)*(e^(-λ))/k!。西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法国数学家、几何学家和物理学家。1781年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇。
4、泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。积分是微分的逆运算,即知道了函数的导函数,反求原函数。
5、泊松积分公式是圆域狄利克雷问题的求解公式。在数学中,狄利克雷边界条件,为常微分方程的“第一类边界条件”,指定微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。
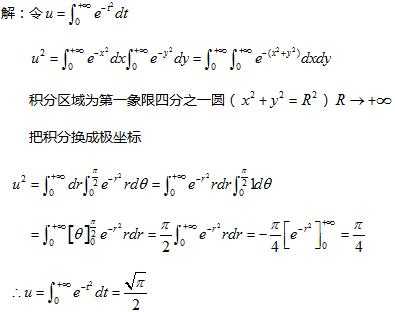
什么是“泊松积分”?
松积分公式是一个重要的数学公式,用于计算维三维的球面分。它由法国数学家西蒙·泊松于19世纪出。
泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。积分是微分的逆运算,即知道了函数的导函数,反求原函数。
泊松公式为:P(k)=(λ^k)*(e^(-λ))/k!。西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法国数学家、几何学家和物理学家。1781年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇。
泊松积分公式是圆域狄利克雷问题的求解公式。在数学中,狄利克雷边界条件,为常微分方程的“第一类边界条件”,指定微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。
泊松积分是怎么证明的
泊松积分是∫[0,+∞]e^(-t)dt=√π/2 泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。
= {(θ,0到2π)∫dθ}*(r,0到∞)∫2e^(-r)dr。= 2π。所以(-∞到∞)∫e^(-x)dx = √(2π)。所以(-∞到∞)∫e^(-x/2)dx =2 √(π)。
你好!这个积分可以直接算出来,它的值是1,所以两边相等。经济数学团队帮你解请及时采纳。
有必要普及一下什么叫极坐标变换了。极坐标,通俗来说就是一个角,一个极径构成的一个坐标系统。
设u(x,y)为平面区域G中的调和函数,且在G的闭包上连续,则借助于平均值公式可以证明,它不能在G 的内部取其最大值与最小值,除非它恒等于一常数。这就是调和函数的最大、最小值原理。
y去不掉。是用极坐标积分得到。或者你可以看下泊松积分。
求泊松积分公式
泊松公式为:P(k)=(λ^k)*(e^(-λ))/k!。西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法国数学家、几何学家和物理学家。1781年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇。
泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。积分是微分的逆运算,即知道了函数的导函数,反求原函数。
= 2π。所以(-∞到∞)∫e^(-x)dx = √(2π)。所以(-∞到∞)∫e^(-x/2)dx =2 √(π)。这个就是泊松积分,并不是泊松积分的一半,其结果等于π^(1/2)/2,建议直接记结果。
泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。泊松积分公式是圆域狄利克雷问题的求解公式。
如何求泊松积分?
∫[-∞,+∞]e^tdt=2∫[0,+∞]e^tdt2∫[0,+∞]dt=+∞ 所以上面的无穷积分是发散的。
= {(θ,0到2π)∫dθ}*(r,0到∞)∫2e^(-r)dr。= 2π。所以(-∞到∞)∫e^(-x)dx = √(2π)。所以(-∞到∞)∫e^(-x/2)dx =2 √(π)。
泊松积分公式是圆域狄利克雷问题的求解公式。公式表明:如果知道调和函数在圆周l上的点(R,θ)的值是u(R,θ),便能找出它在圆内任一点(r,φ)的值。泊松积分公式是圆域狄利克雷问题的求解公式。
这个叫泊松积分。随便找一篇论文就能看到证明。
求概率时,均匀分布量尺寸,正态分布四下子(查表、标准化、对称性、定参数),只有指数分布会用到积分计算。背过两个积分公式——泊松积分和伽马函数。一维随机变量函数的分布。
到此,以上就是小编对于泊松积分的结果的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏