本篇目录:
- 1、菱形是怎么证明的啊?
- 2、怎么证明菱形
- 3、证菱形的方法
- 4、菱形的证明方法是什么
- 5、数学,急急急,证明是菱形
菱形是怎么证明的啊?
1、证明菱形的方法:四条边都相等的四边形是菱形。有一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。对角线互相垂直且平分的四边形是菱形。
2、证明四边相等且对角线相等:如果一个四边形的四条边都相等,且对角线也相等,那么这个四边形就是菱形。这是最常见的证明方法,因为菱形的定义就是四边相等且对角线相等。
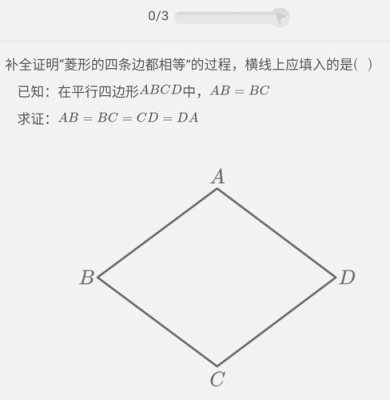
3、定义法:证明菱形的方法之一是根据菱形的定义进行证明。根据定义,菱形是对角线互相垂直且平分的四边形。因此,只需要证明四边形的对角线互相垂直且平分,就可以证明这个四边形是菱形。
怎么证明菱形
1、证明菱形的方法:四条边都相等的四边形是菱形。有一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。对角线互相垂直且平分的四边形是菱形。
2、菱形的证明方法4条:一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。两条对角线分别平分每组对角的四边形。有一对角线平分一个内角的平行四边形。
3、证明四边相等且对角线相等:如果一个四边形的四条边都相等,且对角线也相等,那么这个四边形就是菱形。这是最常见的证明方法,因为菱形的定义就是四边相等且对角线相等。
4、定义法:证明菱形的方法之一是根据菱形的定义进行证明。根据定义,菱形是对角线互相垂直且平分的四边形。因此,只需要证明四边形的对角线互相垂直且平分,就可以证明这个四边形是菱形。
5、菱形的证明如下:一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。四条边均相等的四边形是菱形。对角线互相垂直平分的四边形。两条对角线分别平分每组对角的四边形。
6、所有四条边相等:证明菱形的第一个条件是四条边的长度相等。你可以使用测量工具(如尺子)来测量边长,确保它们的长度一致。对角线互相垂直:证明菱形的第二个条件是对角线互相垂直。
证菱形的方法
1、定义法:证明菱形的方法之一是根据菱形的定义进行证明。根据定义,菱形是对角线互相垂直且平分的四边形。因此,只需要证明四边形的对角线互相垂直且平分,就可以证明这个四边形是菱形。
2、证明菱形的四种方法: 四条边都相等的四边形是菱形。对角线互相垂直且每条对角线平分一组对角。这也是证明菱形的方法。即是菱形。 一个平面内,一组邻边相等的平行四边形是菱形。
3、证明菱形的方法:四条边都相等的四边形是菱形。有一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。对角线互相垂直且平分的四边形是菱形。
4、菱形的证明方法4条:一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。两条对角线分别平分每组对角的四边形。有一对角线平分一个内角的平行四边形。
菱形的证明方法是什么
1、证明四边相等且对角线相等:如果一个四边形的四条边都相等,且对角线也相等,那么这个四边形就是菱形。这是最常见的证明方法,因为菱形的定义就是四边相等且对角线相等。
2、菱形的证明方法4条:一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。两条对角线分别平分每组对角的四边形。有一对角线平分一个内角的平行四边形。
3、定义法:证明菱形的方法之一是根据菱形的定义进行证明。根据定义,菱形是对角线互相垂直且平分的四边形。因此,只需要证明四边形的对角线互相垂直且平分,就可以证明这个四边形是菱形。
4、证明菱形的方法:四条边都相等的四边形是菱形。有一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。对角线互相垂直且平分的四边形是菱形。
5、菱形的证明如下:一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。四条边均相等的四边形是菱形。对角线互相垂直平分的四边形。两条对角线分别平分每组对角的四边形。
6、证明菱形的第三个条件是对角线彼此平分对方。也就是说,两条对角线的交点是对方的中点。你可以使用测量工具来计算对角线之间的距离,确保它们是相等的。如果一个四边形满足以上三个条件,那么它可以被证明为一个菱形。
数学,急急急,证明是菱形
1、定义法:证明菱形的方法之一是根据菱形的定义进行证明。根据定义,菱形是对角线互相垂直且平分的四边形。因此,只需要证明四边形的对角线互相垂直且平分,就可以证明这个四边形是菱形。
2、要证明一个四边形是菱形,我们需要满足以下条件:平行四边形:四边形中有一组对边平行且相等。对角线互相垂直:四边形中对角线互相垂直。例如,假设四边形ABCD中,AB平行且等于CD,对角线AC和BD互相垂直。
3、在同一平面内,一组邻边相等的平行四边形是菱形。在同一平面内,对角线互相垂直的平行四边形是菱形。在同一平面内,四条边均相等的四边形是菱形。在同一平面内,对角线互相垂直平分的四边形是菱形。
4、DF=DF;∴△DEF≌△DCF;∴∠DCF=∠DEF;∴∠DCF=∠EFH;∴EF//CD;(同位角相等,两直线平行)∴四边形CFED是平行四边形;∵有一组邻边相等的平行四边形是菱形;∴四边形CFED是菱形;因此得证。望采纳。
5、解:因为DE∥AC,DF∥AB,所以四边形AFDE是平行四边形。(两组对边分别平行的四边形是平行四边形),因为AD平分∠BAC ,所以AE=DE=DF=AF.,所以四边形AEDF是菱形。
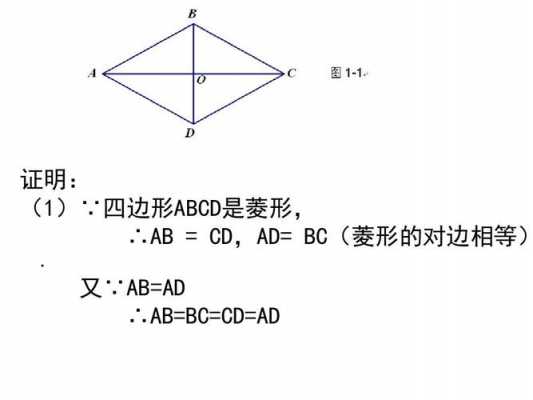
6、证明:因为:平行四边ABCD,所以:EAO=FCO.又因为:EF垂直平分对角线AC,所以:AO=CO、AOE=COF=90度.所以:三角形AOE全等于三角形COF 所以:FO=EO 所以:AC垂直EF且相互平分。所以:四边形AECF是菱形。
到此,以上就是小编对于证明菱形的概念的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏