本篇目录:
- 1、如何快速求解函数值域
- 2、高一数学,值域怎么求,要过程
- 3、值域的求解方法
- 4、求值域解题过程
如何快速求解函数值域
1、换元法 对于函数的某一部分,较复杂或生疏,可用换元法,将函数转变成我们熟悉的形式,从而求解。单调性 可先求出函数的单调性(注意先求定义域),根据单调性在定义域上求出函数的值域。
2、配方法。将函数配方成顶点式的格式,再根据函数的定义域,求得函数的值域。常数分离。一般是对于分数形式的函数来说的,将分子上的函数尽量配成与分母相同的形式,进行常数分离,求得值域。逆求法。换元法。

3、求函数值域的方法如下:观察法 通过对解析式的简单变形和观察,利用熟知的基本函数的值域,求出函数的值域。
4、求函数值域的常用方法有:配方法反解法分离常数法判别式法换元法不等式法函数有界性法直接求函数的值域困难时,可以利用已学过函数的有界性,反客为主来确定函数的值域。
5、直接法:从自变量的范围出发,推出值域。观察法:对于一些比较简单的函数,可以根据定义域与对应关系,直接得到函数的值域。配方法:(或者说是最值法)求出最大值还有最小值,那么值域就出来了。
高一数学,值域怎么求,要过程
高一数学求值域的方法包括:观察法、配方法、判别式法、换元法、数形结合法和基本不等式。观察法:对于一些简单的一次函数,我们可以直接观察图像或者代入特殊值来求得其值域。
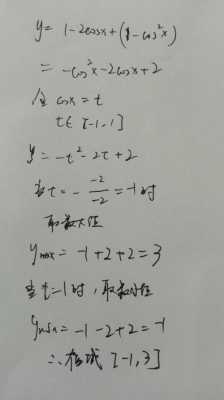
求值域的方法有:直接法:从自变量的范围出发,推出值域;配方法,求出最大值还有最小值;观察法:对于一些比较简单的函数,可以根据定义域与对应关系,直接得到函数的值域等。直接法:从自变量的范围出发,推出值域。
求导,得到y=1-2x^(-2),那么在(0,1]时y‘为负值,所以x=0时函数值最大,等于1时最小。所以值域为[3。
值域的求解方法
三 换元法:利用代数或三角代换,将所给函数化成值域容易确定的另一函数,从而求得原函数的值域,形如 。
图像法 根据函数图象,观察最高点和最低点的纵坐标。配方法 利用二次函数的配方法求值域,需注意自变量的取值范围。单调性法 利用二次函数的顶点式或对称轴,再根据单调性来求值域。

直接法:从自变量的范围出发,推出值域。观察法:对于一些比较简单的函数,可以根据定义域与对应关系,直接得到函数的值域。配方法:(或者说是最值法)求出最大值还有最小值,那么值域就出来了。
此外,这种类型的函数值域也可使用“分离常数法”求解。
求值域解题过程
y=x-√(1-2x).求值域。解:1-2x≥0,得x≤1/观察得,函数在指定区间内为增函数,所以y有最大值,即1/2-√(1-1)=1/所以值域为(-∞,1/2]。判别式法。适用于y是x的2次函数的情况。
。换元法:令t=√(1-2x),则t=0,则1-2x=t^2,2x=1-t^2 x=(1-t^2)/2 所以y=-(t^2)/2-t+1/2(t=0),为二次函数,开口向下,对称轴为t=-所以在[0,+∞)上单调减。
直接观察法 对于一些比较简单的函数,其值域可通过观察得到。配方法 配方法是求二次函数值域最基本的方法之一。
解题步骤:第一步 将二次函数配方成y=a(xb)2+c;第二步 根据二次函数的图像和性质即可求出函数的值域.注意点:要注意函数的定义域,有时候出题人为了迷惑学生,会特意让完全平方式的零点不在定义域内。
图像法 根据函数图象,观察最高点和最低点的纵坐标。配方法 利用二次函数的配方法求值域,需注意自变量的取值范围。单调性法 利用二次函数的顶点式或对称轴,再根据单调性来求值域。
到此,以上就是小编对于求值域的过程咋写的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏