泊松过程应用（泊松过程应用实例）-义乌市趣迅电子商务商行

本篇目录：

泊松过程的性质包括：到达间隔时间列{T，n=1，2，...}是独立同分布的指数随机变量，具有均值1/λ。这些性质使得泊松过程在数学建模和实际问题中有广泛的应用。

泊松分布具有以下特点和性质：均值和方差相等，都等于λ；事件之间的发生是独立的；适用于稀有事件，即λ较小的情况；泊松分布可以作为二项分布的近似。应用领域：泊松分布在许多领域中有广泛的应用。

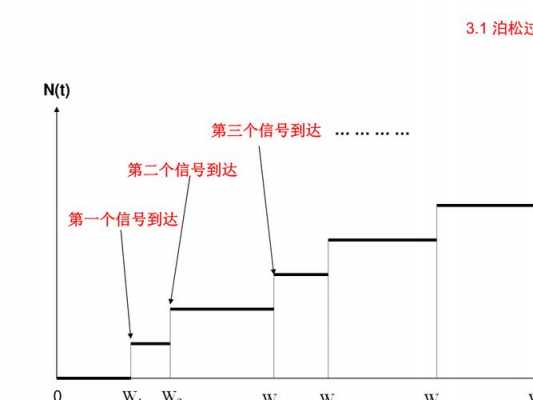
对泊松过程，通常可取它的每个样本函数都是跃度为1的左（或右）连续阶梯函数。

泊松过程是一类较为简单的时间连续状态离散的随机过程。齐次泊松过程是时间空间都为齐次的纯生马尔可夫链；从鞅来看，齐次泊松过程X是使{X(t)-λt，t≥0}为鞅的跃度为1的计数过程。

泊松过程泊松过程有以下几个性质：不相交的时间段上到来的数量是相互独立的；两个点几乎肯定不会同时到达；在某个给定的时间段到达的数量服从泊松分布，分布均值正比于时间段的长度。

1、泊松分布是一种用于描述事件发生次数的离散概率分布。它适用于描述事件不定时发生，但有已知平均发生率的情况。泊松分布具有明确的数学表达式和特性，在许多领域中有重要的应用价值。

2、泊松分布在生产中解决的都是“为宜”的问题，即投入产出的权衡。在实际应用中，还可能会用到“累积概率”，即可以先求出k所对应的各个概率的大小，再计算累积概率的大小。

3、问题：一个服务台每天接待的顾客数服从参数为λ的泊松分布，λ=2。求：（1）一个服务台在10天内接待了1000个顾客的概率；（2）一个服务台在前10天内接待了1000个顾客的概率。

1、泊松过程是随机过程的一种，是以事件的发生时间来定义的。我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程，如果它满足以下条件：在两个互斥（不重叠）的区间内所发生的事件的数目是互相独立的随机变量。

2、泊松过程是一类较为简单的时间连续状态离散的随机过程。齐次泊松过程是时间空间都为齐次的纯生马尔可夫链；从鞅来看，齐次泊松过程X是使{X(t)-λt，t≥0}为鞅的跃度为1的计数过程。

3、若在任一时间区间中发生的事件个数的分布只依赖于时间区间的长度，则称计数过程有平稳增量。

4、或被称为连续时间马尔可夫链。泊松过程是一类较为简单的时间连续状态离散的随机过程，泊松过程在物理学、地质学、生物学、医学、天文学、服务系统和可靠性理论等领域中都有广泛的应用。

到此，以上就是小编对于泊松过程应用实例的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。