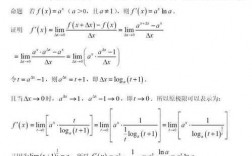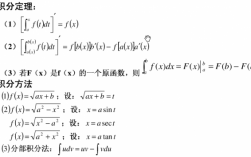本篇目录:
- 1、求y导数,过程详细一点
- 2、如何求函数y的导数?
- 3、y的导数怎么求?怎么算?
- 4、如何求y的导数
- 5、怎么求y的导数?
- 6、隐函数y的导数怎么求?
求y导数,过程详细一点
1、两头取对数,得lny=x lnx再两头对x求导,得1/y *y=lnx+1整理得y=y(lnx+1)将右边的y用x的x次方代替得到y=x^x (lnx+1)。^,指数或次方符号;y,y的导数;ln,以e为底的对数。
2、常用的导数公式包括:(x^n) = nx^(n-1)(sinx) = cosx(cosx) = -sinx(exp(x)) = exp(x)(log(x)) = 1/x使用这些导数公式,可以方便地求出函数的导数。
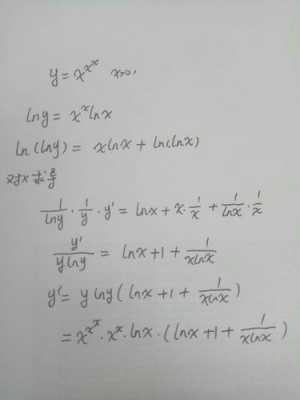
3、导数的定义:当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f(x0)或df(x0)/dx。
4、y=x^(1/x)。lny=1/x*lnx。对x求导:(1/y)*y=(-1/x)*lnx+1/x*1/x=(1-lnx)/x。所以y=x^(1/x)*(1-lnx)/x。导数作用:导数是用来分析变化的。
5、分式函数的求导公式如下:用汉字表示为:(分子的导数*分母-分子*分母的导数)/分母的平方。用字母表示为:(u/v) = (uv-uv)/v。
如何求函数y的导数?
1、y=c,y=0(c为常数)。y=x^μ,y=μx^(μ-1)(μ为常数且μ≠0)。y=a^x,y=a^x lna;y=e^x,y=e^x。y=logax,y=1/(xlna)(a0且a≠1);y=lnx,y=1/x。
2、两头取对数,得lny=x lnx再两头对x求导,得1/y *y=lnx+1整理得y=y(lnx+1)将右边的y用x的x次方代替得到y=x^x (lnx+1)。^,指数或次方符号;y,y的导数;ln,以e为底的对数。
3、例如,对于函数 f(x) = x^2 + sin(x),我们可以先分别求出 x^2 和 sin(x) 的导数,然后相加即可得到 f(x) 的导数。
4、称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。
5、求导得:y/y=2lnx/x y=2x^(-1)(lnx)x^lnx y=2(lnx)x^(lnx-1)不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。

6、分式函数的求导公式如下:用汉字表示为:(分子的导数*分母-分子*分母的导数)/分母的平方。用字母表示为:(u/v) = (uv-uv)/v。
y的导数怎么求?怎么算?
1、y的导数等于y=dy/dx。y=dy/dx,dy可以说是德尔塔y(就是y的变化量)非常小的一个极限。求导数都是y对x的倒数,也就是y,而x对y的倒数其实就是先通过方程式将x用含y的表达式写出来,然后求导,注意变量是y。
2、两头取对数,得lny=x lnx再两头对x求导,得1/y *y=lnx+1整理得y=y(lnx+1)将右边的y用x的x次方代替得到y=x^x (lnx+1)。^,指数或次方符号;y,y的导数;ln,以e为底的对数。
3、常用的导数公式包括:(x^n) = nx^(n-1)(sinx) = cosx(cosx) = -sinx(exp(x)) = exp(x)(log(x)) = 1/x使用这些导数公式,可以方便地求出函数的导数。
4、分式函数的求导公式如下:用汉字表示为:(分子的导数*分母-分子*分母的导数)/分母的平方。用字母表示为:(u/v) = (uv-uv)/v。
如何求y的导数
两头取对数,得lny=x lnx再两头对x求导,得1/y *y=lnx+1整理得y=y(lnx+1)将右边的y用x的x次方代替得到y=x^x (lnx+1)。^,指数或次方符号;y,y的导数;ln,以e为底的对数。
常用的导数公式包括:(x^n) = nx^(n-1)(sinx) = cosx(cosx) = -sinx(exp(x)) = exp(x)(log(x)) = 1/x使用这些导数公式,可以方便地求出函数的导数。
导数的定义:当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f(x0)或df(x0)/dx。
求函数 y 的导数 y 可以使用微积分的方法,具体取决于函数 y 的形式。以下是一些常见情况下的求导方法:常数导数:如果 y 是常数,其导数为 0,即 y = 0。
怎么求y的导数?
1、常用的导数公式包括:(x^n) = nx^(n-1)(sinx) = cosx(cosx) = -sinx(exp(x)) = exp(x)(log(x)) = 1/x使用这些导数公式,可以方便地求出函数的导数。
2、两头取对数,得lny=x lnx再两头对x求导,得1/y *y=lnx+1整理得y=y(lnx+1)将右边的y用x的x次方代替得到y=x^x (lnx+1)。^,指数或次方符号;y,y的导数;ln,以e为底的对数。
3、分式函数的求导公式如下:用汉字表示为:(分子的导数*分母-分子*分母的导数)/分母的平方。用字母表示为:(u/v) = (uv-uv)/v。
隐函数y的导数怎么求?
因此在对方程两边对于X求导时,要把y看成是x的函数,这样就可以得到 e^y*y+y+xy=0 从而得到y=-y/(e^y+x)注:y=dy/dx 如果方程F(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数。
设方程P(x,y)=0确定y是x的函数,并且可导,可以利用复合函数求导公式求出隐函数y对x的导数。
方法①:先把隐函数转化成显函数,再利用显函数求导的方法求导。方法②:隐函数左右两边对x求导(但要注意把y看作x的函数)。方法③:利用一阶微分形式不变的性质分别对x和y求导,再通过移项求得的值。
y=[e^(x+y)-y]/[x-e^(x+y)]隐函数求导方法:先把隐函数转化成显函数,再利用显函数求导的方法求导。隐函数左右两边对x求导。利用一阶微分形式不变的性质分别对x和y求导,再通过移项求得的值。
对于方程F(x,y)=0,假定由此可以确定一个函数,把F(x,y)看成x,y的一个二元函数,那么对于方程左右求导,左边就可以用复合函数的求导法则,右边就是0,再把得到的微分方程变形一下就可以得到隐函数的导数。
到此,以上就是小编对于y的导数求导过程怎么写的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏