本篇目录:
请问什么是布朗运动,什么是维纳过程?
中文名称:布朗运动英文名称:Brownian motion 定义:悬浮在流体中的微粒受到流体分子与粒子的碰撞而发生的不停息的随机运动。
布朗运动是悬浮在液体或气体中的微粒所作的永不停息的无规则运动。它是一种正态分布的独立增量连续随机过程,是随机分析中基本概念之一。其基本性质为:布朗运动W(t)是期望为0方差为t(时间)的正态随机变量。
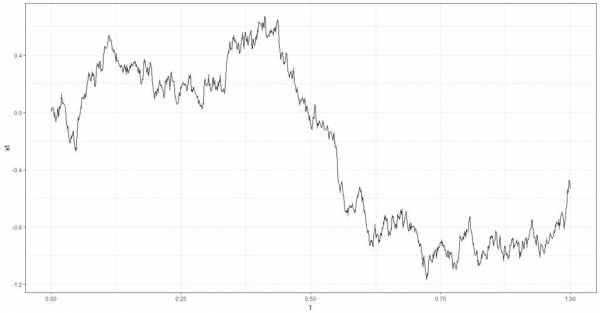
布朗运动是指微小颗粒在流体中无规则运动的现象。布朗运动:布朗运动是由英国植物学家R.布朗于1827年发现的,它是胶体稳定的原因。布朗运动是分子热运动的宏观表现,是一种独特的、随机和无规律的颗粒运动。
随机游动--布朗运动 定义 (1) X(t) 是平稳独立增量过程(X(0) = 0) (2) 每个增量 X(t) - X(s) 服从均值为 0 和方差为 的正太分布,且 布朗运动B(t)又叫维纳过程W(t)。
维纳过程的特点
维纳过程又称布朗运动,它具有如下特点:(1)它是一个Markov过程。因此该过程的当前值就是做出其未来预测中所需的全部信息。(2)维纳过程具有独立增量。
也就是说,对任何的有界连续函数,因此维纳过程具有时间平移不变性:随机过程也是一个维纳过程。不仅如此,维纳过程还满足强马尔可夫性质:对任意的有限停时,随机变量独立于滤波。

{B(t)}布朗运动(brownian motion)也称为维纳过程,是一个随机过程,如果满足以下性质: 独立的增量 对于任意的ts, B(t)-B(s)独立于之前的过程B(u):0=u=s。
数学中,维纳过程是一种连续时间随机过程,得名于诺伯特·维纳。由于与物理学中的布朗运动有密切关系,也常被称为“布朗运动过程”或简称为布朗运动。
⑵ 任意s,t0,X(s+t)-X(s)~N(0,σ^2*t),即X(s+t)-X(s)是期望为0,方差为σ^2*t的正态分布;⑶ X(t)关于t是连续函数。则称{X(t),t=0}是维纳过程(Wiener process)或布朗运动。
根据维纳过程的定义,我们知道W(t)是一个连续时间的高斯过程,其均值为0,协方差函数为Cov(W(s), W(t)) = σ^2 * min(s, t)。

函数发展的历史
1、函数概念是全部数学概念中最重要的概念之一,纵观300年来函数概念的发展,众多数学家从集合、代数、直至对应、集合的角度不断赋予函数概念以新的思想,从而推动了整个数学的发展。
2、函数的发展历程是:运算——解析式——变量的依赖关系或对应关系——映射——集合的对应关系——序偶集。11677年,格列高里:它是从其它的一些量经过一系列代数运算而得到的,或经过任何其他可以想象到的运算而得到。
3、函数的起源历史如下:函数的起源可以追溯到古代,但它作为一个数学概念的明确发展始于 17 世纪。在那个时候,数学家开始尝试用代数方程来描述自然现象,例如行星的运动。
4、伽利略(1564-1642)的落体运动定律、牛顿(1642-1727)的万有引力定律、爱因斯坦(1879-1955)的质能转化公式等等都是用函数概念来表达的。
2012年武汉理工大学博士入学考试《随机过程》考试大纲
随机过程的概念、随机过程的分布函数族、随机过程的数字特征、正交增量过程、独立增量过程、正态过程、维纳过程、复随机过程。考试要求:(1)理解随机过程的概念、掌握随机过程的分布函数族,会求随机过程的数字特征。
考试性质 博士生入学考试是为华中科技大学招收博士研究生而设置的。其中,“矩阵论和随机过程”主要是针对报考计算机类的考生而设置的。
武汉理工大学有工业设计硕士点,在艺术与设计学院,分为专硕和学硕。
维纳过程的一维维纳过程的性质
⑵维纳过程具有独立增量。该过程在任一时间区间上变化的概率分布独立于其在任一的其他时间区间上变化的概率。⑶它在任何有限时间上的变化服从正态分布,其方差随时间区间的长度呈线性增加。
(1)它是一个Markov过程。因此该过程的当前值就是做出其未来预测中所需的全部信息。(2)维纳过程具有独立增量。该过程在任一时间区间上变化的概率分布独立于其在任一的其他时间区间上变化的概率。
数学中,维纳过程是一种连续时间随机过程,得名于诺伯特·维纳。由于与物理学中的布朗运动有密切关系,也常被称为“布朗运动过程”或简称为布朗运动。
不是。根据查询相关信息显示,维纳过程是一个非平稳的高斯过程。维纳过程也叫布朗运动,布朗运动的难点总结二阶矩过程定义:若对任意的t属于T,E[(X(t))2]存在,则称Xt为二阶矩过程。
有限维分布 路径性质 (1)是 t 的连续函数; (2)在任何区间(无论区间多小)上都不是单调的; (3)在任何点都不是可微的。
到此,以上就是小编对于维纳过程平稳过程是什么的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏