本篇目录:
请问:棱锥的体积公式是怎么推导出来的?求解
1、这个公式是通过将棱锥体分解为一个底面积为 A 的平面与一个高度为 h 的三角形棱锥来推导得出的。
2、总之,棱锥体积公式为 (1/3) * B * h,其中 B 表示底面积,h 表示棱锥的高度。

3、(c为底面周长,h_为斜高)。棱锥的体积公式如何推导?推导公式为:S(棱锥)=1/3S(底面积)×H(高)。首先祖_原理是推导过程中的关键,根据这个原理,我们可以将三棱锥变形,放到一个正三棱柱里面。
4、三棱锥体积公式推导如下:首先,将三棱锥分解为一个底面为三角形的锥体和一个顶部为三角锥的棱锥。因此,三棱锥的体积可以表示为这两个部分的体积之和。
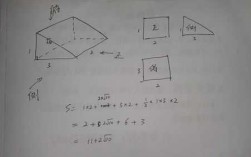
5、解析:根据三棱锥的体积公式,我们可以使用以下计算进行求解:V = (1/3) × 底面积 × 高度首先,计算底面积。三角形的面积可以通过海伦公式或正弦定理来计算。由于这是一个等边三角形,我们可以使用简化的公式。
正三棱锥的侧面积怎么求?
1、面积公式:S侧=(1/2)*C*h,其中:C为底面周长,h是该正棱锥的斜高(即各个侧面等腰三角形底边上的高)三棱锥 三棱锥锥体的一种,几何体,由四个三角形组成。固定底面时有一个顶点,不固定底面时有四个顶点。

2、它的侧面积公式为:S侧=(1/2)乘C乘h。
3、如果三棱锥为正三棱锥,那么它的侧面积公式为:S侧=(1/2)乘C乘h,其中:C为底面周长,h是该正棱锥的斜高。
4、因为是正三棱锥,所以底面是正三角形,侧面是三个等腰三角形。已知侧棱是√2,底边是1。所以可以求得侧面的高=√2-1/4=√7/2。所以侧面积=3×1/2×1×√7/2=3√7/4。
5、已知正三棱锥底面边长是4√3,高为3,求它的侧面积?解:我们知道正三棱锥的底面边长4√3,底面三角形的高就是4√3×√3/2=6,它的1/3与正三棱锥的高、斜高构成直角三角形。

6、既然是正三棱锥,那么侧面都应该是等腰直角三角形。当底面边长为a时,腰长为√2a/2,一个三角形的面积为a/4,该三棱锥的侧面积为3a/4, 侧棱长就是腰长为√2a/2。
棱锥是什么?棱锥的体积怎么算?
1、V 表示棱锥体的体积;A 表示底面的面积;h 表示从底面到顶点的高度。这个公式是通过将棱锥体分解为一个底面积为 A 的平面与一个高度为 h 的三角形棱锥来推导得出的。
2、棱锥的体积公式为:V=Sh/3。在公式中,V为棱锥的体积,S为棱锥底面积,h为底面对应的高。棱锥又称角锥,是三维多面体的一种,由多边形各个顶点向它所在的平面外一点依次连直线段而构成。
3、棱锥体积公式为:V=1/3ah。在几何学上,棱锥又称角锥,是三维多面体的一种,由多边形各个顶点向它所在的平面外一点依次连直线段而构成,多边形称为棱锥的底面。
4、棱锥体积公式为:V=1/3Sh,S为棱锥的底面积,h是高。定义:是指有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥体。
棱锥侧面积公式是什么
正棱锥的侧面积等于底面周长乘以斜高的1/2。一般棱锥只能一个一个的求各个侧面的面积,然后相加。在几何学上,棱锥又称角锥,是三维多面体的一种,由多边形各个顶点向它所在的平面外一点依次连直线段而构成。
如果三棱锥为正三棱锥,那么它的侧面积公式为:S侧=(1/2)乘C乘h,其中:C为底面周长,h是该正棱锥的斜高。
侧面积 = n × 边长 × 斜高 / 2 斜高是指侧面的高度,即从底面到侧面的距离。
正棱锥的侧面积:S侧=(1/2)×C×h1。
四棱锥的侧面积公式
正四棱锥的侧面积公式:S=1/2ch。如果正棱锥的底面周长为c,斜高为h,那么它的侧面积是S=1/2ch。正四棱锥的底面边长为a,体积V=1/3ah。
四棱锥的侧面积:如果正棱锥的底面周长为c,斜高为h,那么它的侧面积是 s=1/2ch。
已知正四棱锥的底面边长为2,斜高为2。首先,我们可以求出底面正方形的面积:2 * 2 = 4。然后,我们可以使用体积公式:V = (底面面积 * 高) / 3,得到体积:V = (4 * 2) / 3 = 67。
到此,以上就是小编对于棱锥棱柱面积公式的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏