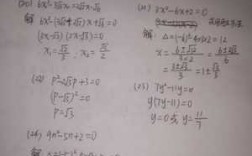本篇目录:
求正弦定理证明
1、正弦定理的证明方法如下:用三角形外接圆证明。作ABC的外接圆O,作直径BD交⊙O于D,连接DA,得∠DAB=90°,则∠D等于∠C,所以c/sinC=c/sinD=BD=2R。类似可证其余两个等式。用直角三角形证明。
2、平方公式:sinx=±√(1-cosx∧2)cosx=±√(1-sinx∧2)诱导公式:sin(π/2+x)=cosx,cos(π/2+x)=—sinx 证明:sinx∧2+cosx∧2=1,移项得sinx∧2=1-cosx∧2,开平方得sinx=±√(1-cosx∧2)。

3、在同一个圆中,对应同一段弧的角相等,即角C=角D,所以c/sinC=c/sinD,ABD为直角三角形,sinD=c/2R,所以c/sinC=c/sinD=2R,同理可证a/sinA=b/sinB=2R。
4、正弦定理公式 a/sinA=b/sinB=c/sinC=2R。【注1】其中“R”为三角形△ABC外接圆半径。下同。【注2】正弦定理适用于所有三角形。初中数学中,三角形内角的正弦值等于“对比斜”仅适用于直角三角形。
5、∴a+b+c=0,则i(a+b+c)=i·a+i·b+i·c =a·cos(180-(C-90))+b·0+c·cos(90-A) =-asinC+csinA=0接着得到正弦定理 定义:正弦定理是三角学中的一个定理。
正弦定理的证明方法
正弦定理的证明方法如下:用三角形外接圆证明。作ABC的外接圆O,作直径BD交⊙O于D,连接DA,得∠DAB=90°,则∠D等于∠C,所以c/sinC=c/sinD=BD=2R。类似可证其余两个等式。用直角三角形证明。

平方公式:sinx=±√(1-cosx∧2)cosx=±√(1-sinx∧2)诱导公式:sin(π/2+x)=cosx,cos(π/2+x)=—sinx 证明:sinx∧2+cosx∧2=1,移项得sinx∧2=1-cosx∧2,开平方得sinx=±√(1-cosx∧2)。
在锐角△ABC中,设BC=a,AC=b,AB=c。
叙述并证明正弦定理
因圆周角相等,即角D=角A,所以sinA=sinD=BC/CD=a/d,同理可证sinB=b/d,sinC=c/d.所以,a/sinA=b/sinB=c/sinC。方法还有一种向量的方法,在旧版课本上。
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。即a/sinA=b/sinB=c/sinC=2R(2R在同一个三角形中是恒量,是此三角形外接圆的半径的两倍)证明:方法在锐角△ABC中,设BC=a,AC=b,AB=c。

证明:任意三角形ABC,作ABC的外接圆O。作直径BD交⊙O于D,连接DA.因为直径所对的圆周角是直角,所以∠DAB=90度,因为同弧所对的圆周角相等,所以∠D等于∠C。所以c/sinC=c/sinD=BD=2R。类似可证其余两个等式。
在同一个圆中,对应同一段弧的角相等,即角C=角D,所以c/sinC=c/sinD,ABD为直角三角形,sinD=c/2R,所以c/sinC=c/sinD=2R,同理可证a/sinA=b/sinB=2R。
证明正弦定理的方法是做一个边长为a,b,c的三角形,对应角分别是A,B,C,从角C向c边做垂线,得到一个长度为h的垂线和两个直角三角形即可。
正弦定理a/sinA=b/sinB=c/sinC推导过程
正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径”,即a/sinA=b/sinB=c/sinC=2r=D(r为外接圆半径,D为直径)。
∴a/sinA=b/sinB=c/sinC=2R 方法2: 用直角三角形 证明:在锐角△ABC中,设BC=a,AC=b,AB=c。
正弦定理公式推导:(1)a=2RsinA;(2)b=2RsinB;(3)c=2RsinC。(1)a:b=sinA:sinB;(2)a:c=sinA:sinC;(3)b:c=sinB:sinC;(4)a:b:c=sinA:sinB:sinC。
a/SinA=b/SinB=c/SinC=2R 做ABC的外接圆,再做直径AD,连接BD,那么ABD是直角三角形并且/_D=/_C,然后就有c/sinC=2R。
到此,以上就是小编对于正弦定理的证明过程完整版的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏