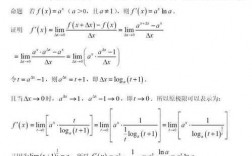本篇目录:
y=arctanx的求导过程
arctanx求导推导:y=arctanx,x=tany,dx/dy=secy=tany+1,dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x)。
arctanx=-arctan(1/x),推导过程分析:y = arctanx,dy/dx = 1/(1 + x),y = -arctan(1/x)dy/dx = -{1/[1 + (1/x)]}×(-1/x)= 1/(1 + x)。

arctanx求导方法:令y=arctanx,则x=tany。
反正切函数的导数公式推导
1、反函数的导数等于直接函数导数的倒数 arccotx=y,即x=coty,左右求导数则有 1=-y*cscy 故y=-1/cscy=-1/(1+coty)=-1/(1+x)。
2、反正切函数的导数是1/(1+x^2)。反正切函数定义为:y= atan(x)或y= arctan(x),它是正切函数的反函数。这意味着,如果y= atan(x),那么x= tan(y)。
3、1/(1-x)=1+x+x^2+x^3+... 1/(1+x^2)=1-x^2+x^4-x^6+...(把-x^2带入第一个里面)。

4、dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x),具体证明过程如下:tanx是正切函数,其定义域是{x|x≠(π/2)+kπ,k∈Z},值域是R。
5、=secy*(y),则 (y)=1/secy 又tany=x,则secy=1+tany=1+x得,(y)=1/(1+x)即arctanx的导数为1/(1+x)。
arctanx的导数是什么?
1、arctanx的导数为1/(1+x)解:令y=arctanx,则x=tany。
2、arctanx的导数:y=arctanx,x=tany,dx/dy=secy=tany+1,dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x)。
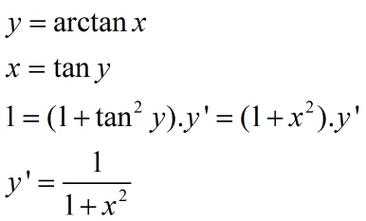
3、解:令y=arctanx,则x=tany。
4、arctanx=x-1/3*x^3+1/5*x^5-1/7*x^7+1/9*x^9+...+(-1)^(n+1)/(2n-1)*x^(2n-1)使用条件:麦克劳林公式无论什么条件下都能使用,关键是展开的项数不能少于最低要求。
5、arctanx求导推导:y=arctanx,x=tany,dx/dy=secy=tany+1,dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x)。
反三角函数导数推导过程
1、反三角函数(inverse trigonometric function)是一类初等函数。指三角函数的反函数,由于基本三角函数具有周期性,所以反三角函数是多值函数。这种多值的反三角函数包括:反正弦函数、反余弦函数、反正切函数、反余切函数。
2、在使用反三角函数时一定要注意其定义值和值域。
3、以y=arcsinx为例,来求反三角函数的求导过程。(根据函数与反函数的导数关系来证明)设函数x=siny,y∈(-π/2,π/2),它的反函数记为为y=arcsinx,x∈(-1,1)函数f=sinx,x∈(-π/2,π/2)上单调,可导。
4、arccotx导数证明过程 反函数的导数等于直接函数导数的倒数 arccotx=y,即x=coty,左右求导数则有 1=-y*cscy 故y=-1/cscy=-1/(1+coty)=-1/(1+x)。
5、一般来说,求导过程是利用dy/dx=1/(dx/dy),然后进行相应的换元。
arctanx的导数怎么求?
1、arctanx的导数:y=arctanx,x=tany,dx/dy=secy=tany+1,dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x)。
2、所以arctanx’=1/tany’而tany’=(siny/cosy)’=(siny’cosy-sinycosy’)/cosy的平方=(cosy的平方+siny的平方)/cos的平方=1+tany的平方=1+x的平方。
3、arctanx求导方法:令y=arctanx,则x=tany。
到此,以上就是小编对于的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏