本篇目录:
函数极值的充要条件是什么?
1、极值的三个充要条件是:函数在该点可导,一阶导数为零,二阶导数为正负。极值点的必要条件:可导性:函数在极值点附近必须是可导的,即函数在该点存在定义并且斜率有限。
2、一个函数能够取到极值(最大值或最小值)的充要条件是其导数在该点处为零或不存在。
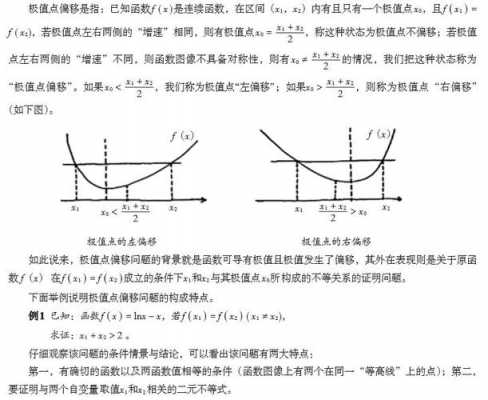
3、一个函数能够取到极值的充要条件是: ①存在使导数等于0的点, 即在该点处 f = 0。②使导数等于0的那个x值,左右两边导数符号相反。若 f左 0,f右 0,则为极大值。
二次函数的极值是怎样求的?
1、二次函数的极值公式是:设二次函数 f(x) = ax^2 + bx + c,其中 a ≠ 0。 如果 a 0,则二次函数的图像开口向上,且函数的最小值(极小值)为 f(-b/2a) = f(x_min) = c - (b^2)/(4a)。
2、②二次函数通过配方或分解因式可求极值。③通过求导是求极值最常用方法。f(x)=0,则此时有极值。0为↑ 0为↓ 判断是极大还是极小值。
3、二次函数y=ax+bx+c(a≠0)求极值有两种方法:直接导入公式:当x=-b/2a时,y极值=4ac-b/4a;利用配方法把一般式转化为顶点式:y=a(x-h)+k,当x=h时,y极值=k。
4、要求二次函数的最大值,可以使用以下方法: 根据二次函数的一般形式 y = ax^2 + bx + c,其中 a、b、c 分别是二次项、一次项和常数项的系数。
5、通过求导求二次函数的最值:对于一般形式的二次函数 f(x) = ax + bx + c,通过求导可以得到它的导函数 f(x) = 2ax + b。
6、二次函数的一般式是y=ax的平方+bx+c,当a大于0时开口向上,函数有最小值;当a小于0时开口向下,则函数有最大值。
求函数极值的一般步骤
首先,计算函数的一阶和二阶导数。找到使得一阶导数为零或不存在的点,这些点同样被称为临界点。然后,通过二阶导数的符号来确定极值类型。
导数求极值步骤:先求导,使导函数等于零,求出x值,确定定义域,画表格,找出极值,注意极值是把导函数中的x值代入原函数。
步骤:确定函数定义域。求导数。在定义域内的单调区间内,令导数等于0,解出临界点的值。判断在临界点左右两侧的导数值的符号,若左侧为负,右侧为正,则该点为极小值点;若左侧为正,右侧为负,则该点为极大值点。
求极大极小值步骤如下:(1)求导数f(x);(2)求方程f(x)=0的根;(3)检查f(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
求函数极值的方法主要有以下几种: 一元函数求极值:对于一元函数f(x),可以通过求导数f(x)为零的点来找到极值点。
多元函数平稳点怎么求
用实对称矩阵求多元函数极值的步骤先求多元函数一阶偏导数,求取稳定点;然后将稳定点代入多元函数对应的矩阵中;判断该矩阵是正定矩阵还是负定矩阵。例2 研究二元函数的极值。解 解方程组得稳定点和。
f(0,0)=0 为最小值!对于多元函数,同样存在极值点的概念。此外,也有鞍点的概念。
当x=y=1/3时z取最小值-2/3,所以点(1/3,1/3)是它的稳定点。
高中数学函数极值,求过程,方法讲解
先求导,然后让导数等于0,得出可能极值点,然后通过判断导数的正负来判断单调性,最后再得出极值,然后再计算端点值,比较大小,最大就是最大值,最小就是最小值。
利用排列组合求极值。[例1] 物体A放在水平面上,作用在A上的推力F与水平方向成30角,如图示。使A作匀速直线运动。
首先,计算函数的一阶和二阶导数。找到使得一阶导数为零或不存在的点,这些点同样被称为临界点。然后,通过二阶导数的符号来确定极值类型。
①首先确定函数定义域。②二次函数通过配方或分解因式可求极值。③通过求导是求极值最常用方法。f(x)=0,则此时有极值。0为↑ 0为↓ 判断是极大还是极小值。
极值的求法:(1)求导数f(x);(2)求方程f(x)=0的根;(3)检查f(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
求函数的极值,要过程步骤
导数求极值步骤:先求导,使导函数等于零,求出x值,确定定义域,画表格,找出极值,注意极值是把导函数中的x值代入原函数。
导数法 步骤:确定函数定义域。求导数。在定义域内的单调区间内,令导数等于0,解出临界点的值。
求函数的最值,即函数的最大值或最小值,主要有以下步骤: 确定函数的定义域:定义域是函数自变量的取值范围,即函数在哪些区间内是有定义的。
求极大极小值步骤如下:(1)求导数f(x);(2)求方程f(x)=0的根;(3)检查f(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
一元函数求极值:对于一元函数f(x),可以通过求导数f(x)为零的点来找到极值点。
求函数 y = f(x) 的极值一般可以按照以下步骤进行:求导:首先,计算函数 f(x) 的导数 f(x)。这一步可以通过微分法或求导法则进行。
到此,以上就是小编对于极值点失稳的特征是结构失稳前后的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏