本篇目录:
用langrange中值定理证明等式arctanx+arctan1/x=π/2
1、-11-23 用拉格朗日中值定理证明arctanx-In(1+x^2)大于... 4 2012-12-21 证明:arctanx+arccotx=2分之派。
2、当xy时,由中值定理知存在c属于区间(x,y),使得arctan (c)=(arctany-arctanx)/(y-x)。而arctan (c)=1/(1+c^2)1,则可得)=|arctany-arctanx||y-x|。当xy时,同理可得。

3、证明一个函数恒等于某个常数,那么对这个函数求导应该是等于0的。
拉格朗日中值定理证明过程
1、拉格朗日定理的证明过程如下:设f(x)在[a,b]连续,(a,b)可导,求证:存在ξ∈(a,b),使f(b)-f(a)=f(ξ)(b-a)。
2、要求点ξ,你需要按照以下步骤进行:首先,确保函数f(x)满足拉格朗日中值定理的前提条件:在闭区间[a, b]上连续,并且在开区间(a, b)内可导。计算函数在区间[a, b]的端点的函数值:f(a)和f(b)。
3、简介:拉格朗日中值定理是微积分中的一条重要定理,它指出如果一个函数在闭区间上连续,在开区间上可导,那么在这个区间内存在至少一点,使得函数的导数在该点上的值等于函数在闭区间上的平均变化率。

罗尔中值定理的证明
1、罗尔中值定理的操作步骤如下:首先,我们需要确定函数的定义域和值域,并证明函数在这个区间内是连续的。然后,我们需要证明函数在这个区间内是可导的。接着,我们需要找到函数在两个点上取到相同的值。
2、证明的思想是构造函数,把斜的化成平的(直观想象)。
3、罗尔(Rolle)中值定理是微分学中一条重要的定理,是三大微分中值定理之一,其他两个分别为:拉格朗日(Lagrange)中值定理、柯西(Cauchy)中值定理。
到此,以上就是小编对于中值定理证明题怎么构造函数的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。
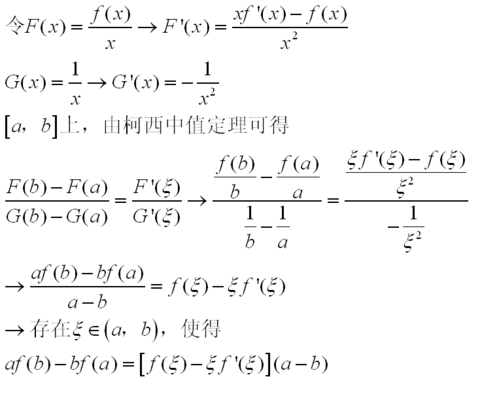

 微信扫一扫打赏
微信扫一扫打赏