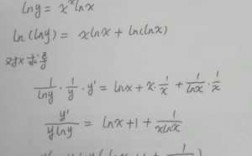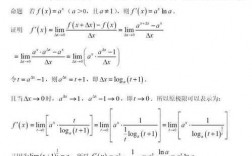本篇目录:
- 1、指数函数求导公式推导过程
- 2、指数函数怎么求导?
- 3、指数函数的导数怎么计算
- 4、指数函数的导数怎么求?
- 5、指数函数的导数公式怎么推导
- 6、如何求指数函数的导数?
指数函数求导公式推导过程
指数函数求导公式推导过程,示例如下:首先回想一下导数的记法,这种基础不能丢。然后在做的过程中,先使用的是指数函数的乘法运算,然后由于a的x0次方是一个常数,所以可以提出来,再采用换元法。
本例子函数为z=x^y,求z对y的偏导数。y=x^(sinx)类型。

设函数y=3^x,则导数y=3^x*ln3 指数函数的求导公式:(a^x)=(lna)(a^x)求导证明:y=a^x 两边同时取对数,得:lny=xlna 两边同时对x求导数,得:y/y=lna 所以y=ylna=a^xlna,得证。
指数函数求导公式是微积分中的重要公式之一,用于计算指数函数的导数。指数函数的一般形式为y = a^x,其中a是常数且大于0,x是自变量。
指数函数怎么求导?
指数函数导数公式:(a^x)=(a^x)(lna)。
指数函数求导公式:(a^x)=(a^x)(lna)。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。指数函数求导公式:(a^x)=(a^x)(lna)。指数函数是重要的基本初等函数之一。

y=f(x)的反函数是x=g(y),则有y=1/x证:显而易见,y=c是一条平行于x轴的直线,所以处处的切线都是平行于x的,故斜率为0。
指数函数的导数怎么计算
1、指数函数求导公式:(a^x)=(a^x)(lna)。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。指数函数求导公式:(a^x)=(a^x)(lna)。指数函数是重要的基本初等函数之一。
2、指数函数的导数可以通过以下步骤计算: 确定指数函数的形式。指数函数通常可以表示为f(x) = a^x,其中a为底数。 使用指数的基本性质,即a^x = e^(x ln a)。其中e是自然对数的底数。
3、指数函数求导公式是微积分中的重要公式之一,用于计算指数函数的导数。指数函数的一般形式为y = a^x,其中a是常数且大于0,x是自变量。

指数函数的导数怎么求?
指数函数导数公式:(a^x)=(a^x)(lna)。
指数函数求导公式:(a^x)=(a^x)(lna)。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。指数函数求导公式:(a^x)=(a^x)(lna)。指数函数是重要的基本初等函数之一。
指数函数的导数可以通过以下步骤计算: 确定指数函数的形式。指数函数通常可以表示为f(x) = a^x,其中a为底数。 使用指数的基本性质,即a^x = e^(x ln a)。其中e是自然对数的底数。
设函数y=3^x,则导数y=3^x*ln3 指数函数的求导公式:(a^x)=(lna)(a^x)求导证明:y=a^x 两边同时取对数,得:lny=xlna 两边同时对x求导数,得:y/y=lna 所以y=ylna=a^xlna,得证。
例如:若 y = 2^x,那么 dy/dx = 2^x * ln(2)。需要注意的是,幂函数和指数函数的导数公式是微积分中的基本公式之一,通过它们可以求出在某一点的导数值,进而进行曲线的切线斜率、最值、拐点等相关计算。
指数函数的导数公式怎么推导
1、指数函数求导公式推导过程,示例如下:首先回想一下导数的记法,这种基础不能丢。然后在做的过程中,先使用的是指数函数的乘法运算,然后由于a的x0次方是一个常数,所以可以提出来,再采用换元法。
2、指数函数求导公式:(a^x)=(a^x)(lna)。指数函数是重要的基本初等函数之一。一般地,y=ax函数(a为常数且以a0,a1)叫做指数函数,函数的定义域是 R 。
3、为了理解这个公式,我们可以通过一些推导和解释来说明。
4、这意味着幂函数的导数是常数乘以自变量的幂次减一。这些求导公式是微积分中的基本规则,可以用于计算指数函数和幂函数的导数。它们在数学、物理、工程等领域中广泛应用,用于解决与变化率、斜率和曲线的性质相关的问题。
5、我们可以利用二项式展开来展开(x+h)^n,并对其中的高次项进行化简,然后取极限h-0,最终得到f(x) = nx^(n-1)。 指数函数的导数:对于指数函数f(x) = e^x,导数为f(x) = e^x。
如何求指数函数的导数?
1、指数函数导数公式:(a^x)=(a^x)(lna)。
2、指数函数求导公式:(a^x)=(a^x)(lna)。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。指数函数求导公式:(a^x)=(a^x)(lna)。指数函数是重要的基本初等函数之一。
3、指数函数的导数可以通过以下步骤计算: 确定指数函数的形式。指数函数通常可以表示为f(x) = a^x,其中a为底数。 使用指数的基本性质,即a^x = e^(x ln a)。其中e是自然对数的底数。
4、如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。由设的辅助函数可以知道:△x=loga(1+β)。
到此,以上就是小编对于指数求导法则公式推理的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏