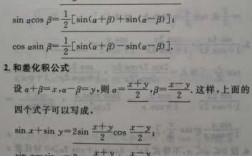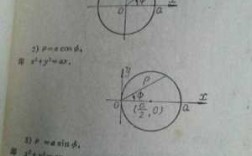本篇目录:
同角三角函数的推理过程?
1、同角三角函数关系可以通过三角恒等式来证明。以下是几个常见的同角三角函数关系的证明: 正弦函数的证明: 根据单位圆的定义,对于任意角度θ,假设在单位圆上选择一点P(x, y),其对应的角度为θ。
2、sin(α+β)推导过程如是:sin(a+b)=cos(π/2-(a+b))=cos((π/2-a)-b)=cos(π/2-a)cosb+sin(π/2-a)sinb =sinacosb+cosasinb。

3、正切函数的性质:正切函数是一个周期函数,其周期为π;正切函数是一个奇函数,即tan(-θ) = -tanθ;正切函数还是一个连续函数。
4、同角三角函数关系六角形记忆法 构造以“上弦、中切、下割;左正、右余、中间1”的正六边形为模型。倒数关系 对角线上两个函数互为倒数;商数关系 六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
5、先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
求这第三题的几何推理的过程。。。
1、因为AB//DC,所以异面直线AE和CD所成角的平面角为角EAB。设AB=a,则PD=BD=(根号2)a,PB=2a,PE=EB=a,则AB=EB。PB=2a,AB=a,在直角三角形PAB内,角ABP=60度。所以三角形ABE是等边三角形。

2、证明:连接OC。∵OC=OA,∴∠OCA=∠OAC。∵AC平分∠DAB,∴∠CAD=∠OAC。∵∠OCA=∠OAC,∠CAD=∠OAC。∴∠CAD=∠OCA,∴OC//AD。∵AD⊥DC,∴OC⊥DC。∴DC为圆O的切线。
3、∵OCD平分∠AOB,PC⊥OA,PH⊥OB,∴PE=PH=2。解:∠B=∠CAF。理由:∵EF垂直平分AD,∴AF=DF,∴∠FAD=∠FDA,∵∠FAD=∠DAC+∠CAF,∠FAD=∠B+∠DAB,又∠DAB=∠DAC,∴∠B=∠CAF。
4、世纪有一个人叫旺策尔,证明了这个题目光用尺规是作不出来的。证明这个几何题目的方法,竟然是代数。 推理方法很值得借鉴。
5、要让学生认识到图形的认识与测量有密切关系,在推导一些常见图形周长、面积、体积计算方法的过程中,感悟数学度量方法,逐步形成量感和推理意识。图形的运动 平移:平移不改变图形的形状和大小。

6、第五题:貌似还得是正多边形?内角和是外角和的3倍,既一个内角是他相邻的外角的3倍,很容易求出来这个多边形的内角为135°,先求出这个多边形的边数=再用上面的公式。可求出这多边形的对角线有20。
当哪两个角相等时,AD∥BC?写出你的推理过程
1、∠3和∠4跟AD和BC一点关系也没有。在图中,∠3和∠4的位置关系是内错角,它们都有一个公共边BD,而AB和CD分别在BD的两侧,且∠3和∠4方向相对,这样的角就叫做内错角。当内错角相等时,内错角的非公共边平行。
2、已知:在梯形ABCD中,AD//BC,AB=CD。
3、(1)找出“性质1”的题设和结论,画出的图形,写出已知和求证。 (2)证明角和角相等有哪些方法?(学生可能会想到平行线的性质,全等三角形的性质) (3)通过折叠等腰三角形纸片,你认为本题用什么方法证明∠B=∠C,写出证明过程。
4、这是一个假命题。平行于于梯形底边的直线截两腰所得的梯形与原梯形不会是相似梯形。
5、首先,我们需要了解等腰直角三角形的定义。等腰直角三角形是指,这个三角形有两个角是相等的,且其中一个角是 90 度。接下来,我们来证明一下为什么等腰直角三角形的两个底角相等。
6、要证明两角相等,这对于刚学习推理证明的学生来说并非易事。要回忆至今为止已经学过的关于两个角相等的定理,联想到“同角的补角相等”这个定理,从而受到启发获得证明的思路。
同角三角函数间的关系知识点
同角三角函数之间的基本关系如下:正弦函数的平方和余弦函数的平方、正切函数的平方和余切函数的平方、正割函数的平方和余割函数的平方都等于1 。正弦函数与余割函数、正切函数与余切函数、余弦函数与正割函数互为倒数。
三角函数商数关系:tanα=sinα/cosα;cotα=cosα/sinα。平方关系:sinα+cosα=1;1+tanα=secα;1+cotα=cscα。
三角函数倒数关系:tanαcotα=1;sinαcscα=1;cosαsecα=1。三角函数商数关系:tanα=sinα/cosα;cotα=cosα/sinα。
三角函数推导过程
1、三角函数的推导过程是建立直角三角形坐标系、利用勾股定理推导、正弦余弦函数的推导。建立直角三角形坐标系:为了推导三角函数,我们需要在直角三角形中建立一个坐标系。以直角顶点为原点,水平方向为x轴,垂直方向为y轴。
2、三角函数推导过程如下:tan(α+β)=sin(α+β)/cos(α+β)=(sinα cosβ + cosα sinβ)/(cosα cosβ - sinα sinβ)=(tanα + tanβ)/(1 - tanα tanβ)(上下同除cosα cosβ)。
3、∴f(x)是一个常数 代入x=1得:f(x)=f(1)=arctan1+arctan1=π/4+π/4 =π/2 即:arctanx+arctan(1/x)=π/2 常见的三角函数包括正弦函数、余弦函数和正切函数。
到此,以上就是小编对于同角的性质的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏