随机过程概率密度（随机过程概率密度函数）-义乌市趣迅电子商务商行

本篇目录：

严平稳过程一定是宽平稳过程，反之，不一定。但对于正态随机过程两者是等价的。后面，若不加特别说明，平稳过程均指宽平稳过程。联合宽平稳随机过程：若，是宽平稳过程，且其中：。则称和为联合宽平稳随机过程。

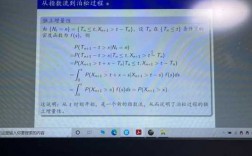
X(t2)，···，X(tn)）和（X(t1+h)，X(t2+h)，···，X(tn+h)）具有相同的分布函数，则称随机过程{X(t)，t∈T}具有平稳性，称此过程为严平稳随机过程，简称随机过程。

一个随机过程平稳表明该过程进入一种稳态。严平稳是一种条件比较苛刻的平稳性定义，它认为只有当序列所有的统计性质都不随着时间的推移而发生变化时，该序列才能被认为平稳。

在数学中，平稳随机过程或者严平稳随机过程又称狭义平稳过程。

几乎平稳”的。因此，宽平稳过程不要求对于任意的时间差(t2-t1)，其对应的随机变量的联合分布函数都相同，只要时间差较小的时候差别不太大即可。因此，严平稳过程不一定是宽平稳过程，而宽平稳过程也不一定是严平稳过程。

1、Exp指的是指数分布，而括号中的0.5就是此分布的参数，x服从参数0.5的指数分布。如果一个随机变量呈指数分布，当s，t0时有P（Tt＋s｜Tt）=P（Ts）。

2、y=g(x)=e^(-λx)f(y) = f(x)/|g(x)| = λe^(-λx)/|-λe^(-λx)| = 即， Y 在[0，1]上均匀分布。

3、所以Fy(y)是上式的积分，为1-1/y，(y=1)所以fy(y)是上式的导数，为1/y^2，(y=1)，其余为0。由于随机变量X的取值只取决于概率密度函数的积分，所以概率密度函数在个别点上的取值并不会影响随机变量的表现。

4、若f(x)=λexp(-λx)，则称X服从参数为λ的指数分布。其中λ0是分布的一个参数，常被称为率参数（rateparameter）。即每单位时间内发生某事件的次数。指数分布的区间是[0，∞)。

5、设X~E(λ)，则其密度函数f(x)=λe^(-λx)，x0、f(x)=0，x≤0。根据定义，其特征函数Φ[x(t)]=E[e^(i tX)]=∫(0，∞)[e^(itx)]f(x)dx=λ∫(0，∞)[e^(itx-λx)]dx。

你如果把整个随机过程看成是一个无穷维度的随机向量，那它就有概率密度函数。

你好！离散型随机变量没有概率密度，与连续型随机变量的概率密度地位相当的就是概率表（或分布律）。经济数学团队帮你解请及时采纳。

离散型的分布函数F（x），是以x为右端点所有左边随机变量取值的概率求和；连续型的分布函数F（x），是以x为右端点所有左边随机变量密度函数的积分。

到此，以上就是小编对于随机过程概率密度函数的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。