本篇目录:
为什么泊松过程是非平稳随机过程
1、区别:泊松过程是一类较为简单的时间连续状态离散的随机过程。复合泊松过程是由对泊松过程的每一点赋予一独立同分布的随机变量而得的随机过程。
2、生灭过程,是一种特殊的离散状态的连续时间马尔可夫过程,或被称为连续时间马尔可夫链。
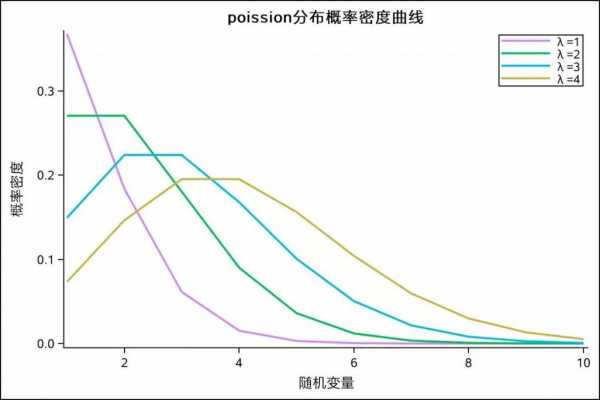
3、泊松过程:泊松分布的概念还引申出了泊松过程。泊松过程是一种连续时间的随机过程,用于描述一系列相互独立的事件的发生。泊松过程在排队论、风险分析、金融模型等方面有重要应用。
4、泊松过程是马尔可夫过程之一,首先独立增量过程是一种特殊的马尔可夫过程,泊松过程和维纳过程是两种最重要的独立增量过程,是研究热噪声和散弹噪声的理论基础。所以泊松也是属于马尔可夫过程的。
5、平稳信号和非平稳信号都是随机信号,区别在于特性和定义不同。随机信号是随机过程,其每个时间点都是一个随机变量。
连续型随机变量分布有哪几种
1、常见的连续型随机变量有:均匀分布随机变量:均匀分布随机变量是指取值概率在一段区间内相等的随机变量。
2、两点分布(伯努利分布)定义:一个非常简单只有两个可能结果的试验,比如正面或反面,成功或失败,有缺陷或没有缺陷,病人康复或未康复。
3、正态分布:概率密度f(x)=[1/(2πσ)^0.5]*e^[-(x-μ)^2/2σ^2],x∈(-∞,+∞),期望EX=μ,方差DX=σ。指数分布:概率密度f(x)=λe^(-λx),(x0)。期望EX=1/λ,方差DX=1/λ^2。
4、随机变量分离散型和连续型。离散型随机变量的值是有限个,主要包括两点分布,二项分布,超几何分布等几种。连续型随机变量没有值,只有概率密度函数。
5、正态概率分布 (normal probability distribution)描述连续型随机变量的一种概率分布。
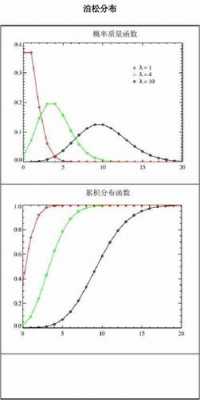
泊松分布的概率公式是什么?
1、泊松分布公式:P{X=k}=λ^k/(k!e^λ)。
2、泊松公式为:P(k)=(λ^k)*(e^(-λ))/k!。西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法国数学家、几何学家和物理学家。1781年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇。
3、泊松分布公式是Var(x)=λ。二项分布的期望E(r)=np,方差Var(r)=npq,而泊松分布的期望和方差均为λ。此时我们需要这两种分布的期望和方差相近似,即np与npq近似相等的情况。
4、泊松分布的概率密度函数为: P(X=k) = (λ^k * e^(-λ)) / k。泊松分布,也就是Poisson分布,是一种统计与概率学里常见到的离散概率分布。
5、泊松分布公式:随机变量X的概率分布为:P{X=k}=λ^k/(k!e^λ) k=0,1,..则称X服从参数为λ(λ0)的泊松分布,k代表的是变量的值,且是自然数。
6、泊松分布概率密度公式:F=G/n。泊松分布是一种统计与概率学里常见到的离散机率分布。泊松分布是以18~19世纪的法国数学家西莫恩·德尼·泊松命名的,他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。
泊松分布概率问题
泊松分布是一种用于计算事件发生次数的概率分布。它的名称来源于法国数学家西蒙·丹尼·泊松(Siméon-DenisPoisson),他在1837年首次提出了这个分布。
泊松分布在生产中解决的都是“为宜”的问题,即投入产出的权衡。在实际应用中,还可能会用到“累积概率”,即可以先求出k所对应的各个概率的大小,再计算累积概率的大小。
P(x)=(m^x/x!)*e^(-m)p ( 0 ) = e ^ (-m)称为泊松分布。例如采用0.05J/m2紫外线照射大肠杆菌时,每个基因组(~4×106核苷酸对)平均产生3个嘧啶二体。
泊松分布(Poisson distribution),台译卜瓦松分布,是一种统计与概率学里常见到的离散机率分布。泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松命名的,他在1838年时发表。
非齐次泊松过程请问什么是非齐次泊松分布,能举例说明
1、这两者不是一个概念,首先“概率分布”这个东西描述的是一个频率呈现的状态。二项分布和泊松分布本身是则是两种不同的概率状态。但是,在特定的时候,即当二项分布的n很大而p很小,他们两者的状态是很相近的,近似一样。
2、概率论中常用的一种离散型概率分布。若随机变量 X 只取非负整数值,取k值的概率为λke-l/k!(记作P (k;λ),其中k可以等于0,1,2,则随机变量X 的分布称为泊松分布,记作P(λ)。
3、泊松过程是一类较为简单的时间连续状态离散的随机过程。齐次泊松过程是时间空间都为齐次的纯生马尔可夫链;从鞅来看,齐次泊松过程X是使{X(t)-λt,t≥0}为鞅的跃度为1的计数过程。
4、非齐次泊松过程可通过时间尺度的变换变为齐次泊松过程。对泊松过程,通常可取它的每个样本函数都是跃度为1的左(或右)连续阶梯函数。
5、我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程,如果它满足以下条件:在两个互斥(不重叠)的区间内所发生的事件的数目是互相独立的随机变量。
到此,以上就是小编对于泊松过程 均匀分布的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏