本篇目录:
正十二边形面积怎么求?
正十二边形的面积公式=3r 。在几何学中,十二边形是指有十二条边和十二个顶点的多边形,其每个内角为150°,内角和为1800°。十二边形有很多种,其中对称性最高的是正十二边形。
正八边形 周长=8(2-21/2)1/2*R, 面积=2*21/2*R2 正十二边形 周长=12*(2-31/2)1/2*R, 面积=3R2 比较圆的周长和面积公式,我们也可以看到许多的相似之处,周长=2πR,面积= πR2。
假设12边型边长为r 那么就可以把12边型看做是12个等腰三角形。
正十二边形的面积,一般来说可以分割成面积大小相同的12个三角形,然后先计算这一个三角形的面积,再累加这12个三角形的面积就得到了这个正12边形面积。
右半部分是个顶角30度的直角三角形,因此面积为四分之根号六R的平方。解得R平方=根号三分之八。正十二边形面积为十二个小三角形面积之和,正弦定理算面积,所以最终总面积为八倍根号三。
扇形面积公式推导过程
扇形面积公式推导过程如下:由定理“等半径的两个扇形的面积之比等于它们的弧长之比”,将圆看作扇形,利用弧长公式和圆的面积公式即可。扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。

扇形面积公式是S=nπR/360或S=LR/2,其中π是圆周率,R是底圆的半径,n是圆心角的度数,L为弧长。n度扇形所对应的弧长为:L=n2πR/360。
扇形面积公式是计算扇形面积的一种方法。扇形是由一条弧和两条半径所组成的图形,其面积计算涉及到圆的面积和角度。
人教版五年级上册数学《组合图形的面积》教案
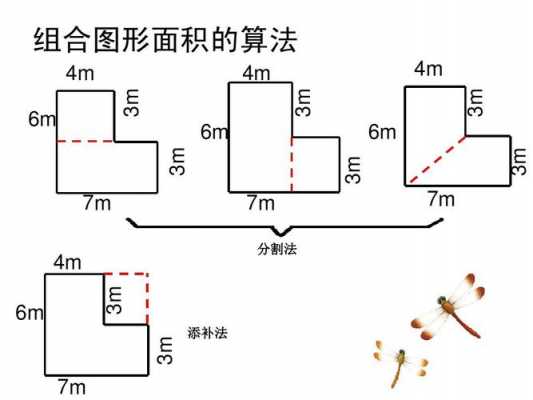
在探索活动中,理解组合图形面积计算的多种方法,会利用正方形、长方形、平行四边形、三角形、梯形这些平面图形面积来求组合图形的面积。 教学难点: 根据图形特征采用什么方法来分解组合图形,达到分解的图形既明确而又准确求出它的面积。
探索组合图形面积的计算方法。 教师引导:大家真了不起,知道生活中存在着这么多的美丽组合图形,那如果我们想知道这些组合图形有多大,实际上是求什么?现在我们就来探讨组合图形的面积计算方法。

组合图形面积是在长方形、正方形、平行四边形、三角形和梯形这五个基本图形的面积公式学习之后,进行的一种由形象到抽象的学习。
小学五年级数学《组合图形的面积》课件篇一 教学目标: 在自由探索的活动中,理解计算组合图形面积的各种方法。 能根据各种组合图形的条件,有效地选择计算方法并正确解 能运用所学的知识,解决生活中组合图形的实际问题。
《组合图形面积》五年级上册《多边形面积》这一单元的内容。这一单元教材包括四部分内容:平行四边形的面积、三角形的面积、梯形的面积和组合图形面积。
《义务教育课程标准实验教科书数学》(人教版)五年级上册“组合图形的面积” 教学目标: 明确组合图形的意义,掌握用分解法或添补法求组合图形的面积。 能根据各种组合图形的条件,有效地选择计算方法并进行正确的解
多边形的面积怎么算?
1、多边形有很多种,不同的多边形面积计算公式不同。
2、平行四边形的面积=底×高。计算公式:S=a×h。三角形的面积=底×高÷2。计算公式:S=a×h÷2。梯形的面积=(上底+下底)×高÷2。计算公式:S=(a+b)×h÷2。正方形的面积=边长×边长。
3、规则多边形面积。面积=1/2 x周长x边心距。这个公式的解释如下:周长:所有边长的总和。边心距:多边形的中心到各边的垂直距离。如果题目让你用的是边心距方法,一般来说题里都会给出边心距的大小。
4、求多边形的面积需要先将不规则多边形分解成熟悉的图形三角形、正方形等规则图形。然后套用公式,将各个规则图形面积解出。最后将所有图形面积进行求和计算即可得出多边形面积。
到此,以上就是小编对于组合图形面积推导过程怎么写的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏