本篇目录:
圆锥的体积公式如何推导,详细过程。
圆锥体积的推导过程如下:圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
推导过程如下:三棱锥2的底ΔABA’、ΔB’A’B的面积相等,高也相等(顶点都是C)。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等,高也相等.(顶点都是A’)。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。
下面是圆锥体积公式推导过程:需要知道一个基本的数学知识,即立方体的体积公式:V=a×a×a=a^3,其中a是立方体的边长。这个公式是体积计算的基础,将其作为出发点。要了解圆锥的基本定义和属性。
高中圆锥体积公式推导过程证明:我们可以使用微积分的方法推导圆锥体积公式。设圆锥底面半径为r,高为h,母线长为l。根据圆锥的定义,可知圆锥的体积为:V=1/3×底面积×高。
圆锥体积公式推导过程是什么?
1、圆锥体积的推导过程如下:圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
2、推导过程如下:三棱锥2的底ΔABA’、ΔB’A’B的面积相等,高也相等(顶点都是C)。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等,高也相等.(顶点都是A’)。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。
3、下面是圆锥体积公式推导过程:需要知道一个基本的数学知识,即立方体的体积公式:V=a×a×a=a^3,其中a是立方体的边长。这个公式是体积计算的基础,将其作为出发点。要了解圆锥的基本定义和属性。
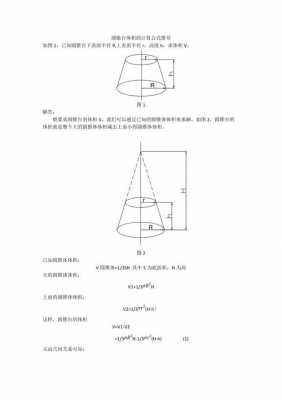
4、圆锥体的体积由圆柱推导而来。设 h为圆台的高, r和R为棱台的上下底面半径, V 为圆台的体积。
圆锥的公式是怎么推导的?
圆锥体积的推导过程如下:圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
推导过程如下:三棱锥2的底ΔABA’、ΔB’A’B的面积相等,高也相等(顶点都是C)。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等,高也相等.(顶点都是A’)。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。
我们可以使用微积分的方法推导圆锥体积公式。设圆锥底面半径为r,高为h,母线长为l。根据圆锥的定义,可知圆锥的体积为:V=1/3×底面积×高。
圆锥的公式可以通过几何推导得出。具体而言,以圆锥顶点为顶点,将圆锥投影为一个直角三角形或者一个斜三角形。如果是直角圆锥,则底面和平面母线垂直;如果是斜圆锥,则底面和平面母线呈一般角。
高中圆锥体积公式推导过程证明
推导过程如下:三棱锥2的底ΔABA’、ΔB’A’B的面积相等,高也相等(顶点都是C)。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等,高也相等.(顶点都是A’)。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。
圆锥的体积公式推导过程为:圆锥的体积=圆柱体积÷3,而圆柱的体积=底面积×高,所以圆锥的体积V=底面积×高÷3。
圆锥体积的推导过程如下:圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
下面是圆锥体积公式推导过程:需要知道一个基本的数学知识,即立方体的体积公式:V=a×a×a=a^3,其中a是立方体的边长。这个公式是体积计算的基础,将其作为出发点。要了解圆锥的基本定义和属性。
圆锥体积公式为 V=1/3sh,其中V表示体积,s表示底面积,h表示高。这个公式可以由下面的推导过程得出:将圆锥沿着中心对称轴切开,得到一个圆柱和两个相等的圆锥形切片。这个圆柱的底面积和高度与原始圆锥相等。
圆锥体积公式怎么推导的?
圆锥体积的推导过程如下:圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
一个圆锥的体积等于与它等底等高的圆柱的体积的1/3,根据圆柱体积公式V=Sh(V=rrπh),得出圆锥体积公式:圆锥V=1/3Sh。S是圆锥的底面积,h是圆锥的高,r是圆锥的底面半径。证明:把圆锥沿高分成k分,每份高h/k。
圆锥体的体积由圆柱推导而来。设 h为圆台的高, r和R为棱台的上下底面半径, V 为圆台的体积。
下面是圆锥体积公式推导过程:需要知道一个基本的数学知识,即立方体的体积公式:V=a×a×a=a^3,其中a是立方体的边长。这个公式是体积计算的基础,将其作为出发点。要了解圆锥的基本定义和属性。
根据圆柱体积公式V=Sh(V=rrπh),得出圆锥体积公式:圆锥 V=1/3Sh S是圆锥的底面积,h是圆锥的高,r是圆锥的底面半径。
用极限法可以推导: V=1/3Sh(V=1/3SH)S是底面积,h是高,r是底面半径。设圆锥高为h,底部半径为r,把圆锥等分为k份,每份看做一个小圆柱。则第n份圆柱的高为h/k, 半径为n*r/k。
圆锥体积推导过程图解
推导过程如下:三棱锥2的底ΔABA’、ΔB’A’B的面积相等,高也相等(顶点都是C)。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等,高也相等.(顶点都是A’)。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。
圆锥体积公式为 V=1/3sh,其中V表示体积,s表示底面积,h表示高。这个公式可以由下面的推导过程得出:将圆锥沿着中心对称轴切开,得到一个圆柱和两个相等的圆锥形切片。这个圆柱的底面积和高度与原始圆锥相等。
下面是圆锥体积公式推导过程:需要知道一个基本的数学知识,即立方体的体积公式:V=a×a×a=a^3,其中a是立方体的边长。这个公式是体积计算的基础,将其作为出发点。要了解圆锥的基本定义和属性。
圆锥体积的推导过程是通过一个倒水实验来推导的。需要准备两个等底等高的圆柱和圆锥容器,在圆锥容器里倒满水,再往圆柱容器里倒,就会发现需要倒3次才能将这个圆柱容器刚好倒满。
到此,以上就是小编对于圆锥的计算推导过程是什么的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏