本篇目录:
如何证面面平行的判定定理
面面平行的判定定理的证明方法有反证法、判定定理、向量法。反证法 假设这两个平面不平行,那么它们相交,设交线为l。∵a∥β ∴a与β无交点。同理,b与β无交点。∵l是两个平面的交线,l?β。
面面平行的判定定理为如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行;如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
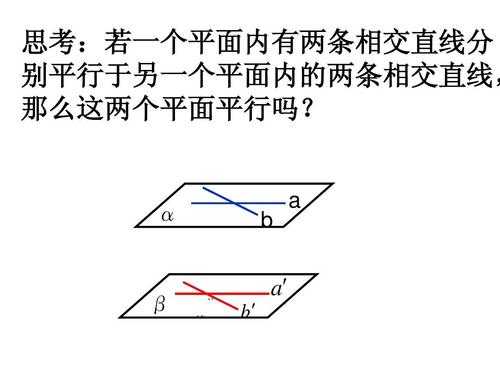
∴假设不成立,α∥β 推论 如果两个平面的垂线平行,那么这两个平面平行。(可理解为法向量平行的平面平行)证明:由线面垂直的性质可知两条平行线与两个平面都垂直,运用定理1可知面面平行。
面面平行的证明方法为:面面平行的判定定理为如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行;如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
如果两个平面垂直于同一条直线,那么这两个平面平行。如果一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行。
面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。

证明面面平行的方法
一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,明两个平面没有公共点。
一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,证明两个平面没有公共点。
面面平行政证明方法有如下:面面平行的判定定理:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
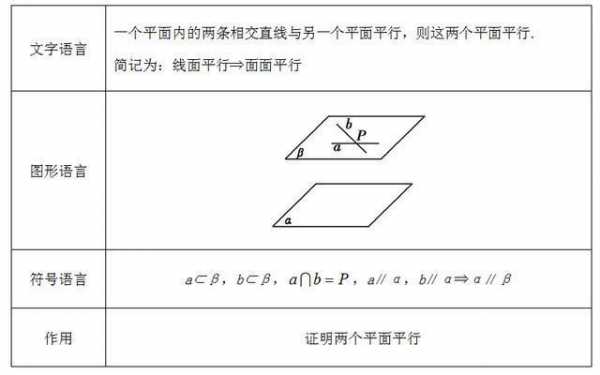
面面平行的性质定理如下:定理1:两个平面平行,在一个平面内的任意一条直线平行于另外一个平面。
以下是面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
面面平行的证明方法
1、面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
2、以下是面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
3、证明面面平行的方法如下:根据定义。证明两个平面没有公共点。由于两个平面平行的定义是否定形式,所以直接判定两个平面平行较困难,因此通常用反证法证明。根据判定定理。
4、证明面面平行的方法如下:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。如果一个平面内垂直于两个平面的交线的直线与另一个平面平行,那么这两个平面平行。
5、一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,证明两个平面没有公共点。
6、面面平行的证明方法为:面面平行的判定定理为如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行;如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
怎么证面面平行的
1、如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。如果一个平面内垂直于两个平面的交线的直线与另一个平面平行,那么这两个平面平行。
2、一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,证明两个平面没有公共点。
3、面面平行政证明方法有如下:面面平行的判定定理:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
面面平行怎么证
1、如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。如果一个平面内垂直于两个平面的交线的直线与另一个平面平行,那么这两个平面平行。
2、一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,证明两个平面没有公共点。
3、定理及其推论是向量法证明面面平行的基础,如果两个平面的法向量平行或相等,那么这两个平面平行。如果一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行。
4、面面平行政证明方法有如下:面面平行的判定定理:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
5、面面平行的性质定理如下:定理1:两个平面平行,在一个平面内的任意一条直线平行于另外一个平面。
6、定理1及其推论是向量法证明面面平行的基础,如果两个平面的法向量平行或相等,那么这两个平面平行。定理2:如果一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行。
如何证明面面平行
1、面面平行政证明方法有如下:面面平行的判定定理:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
2、面面平行的证明方法:面面平行的判定定理:如果一个平面内有两条相交,直线都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。
3、一般有三种方法:如果一个平面内有两条相交直线与都平行于另一个平面,那么这两个平面平行。如果两个平面都垂直同一条直线,那么这两个平面是互相平行的。根据两个平面平行的定义,证明两个平面没有公共点。
到此,以上就是小编对于面面平行的证明方法的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏