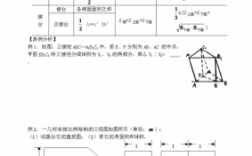
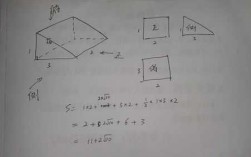
本篇目录:
三角形的面积推导过程
1、找到三角形两边的中点,分别做垂线,并沿垂线剪下,得到两个小三角形,通过平移,可以得到一个长方形。
2、根据公式:三角形面积=(底×高)/2 可知:底×高=2面积;底=三角形面积×2÷高;高=三角形面积×2÷底。(面积=底×高÷2。
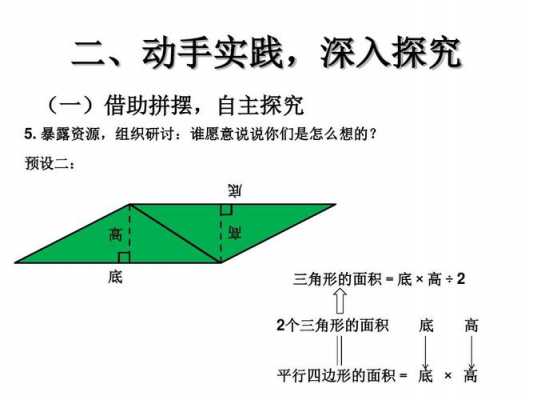
3、根据等边三角形的推导过程,我们可以得知,三角形ABD和ACD的面积分别为(√3/4)*AB^2和(√3/4)*C^2。使用三角函数计算三角形的面积 除了使用底边长和高来计算三角形的面积外,我们还可以利用三角函数来计算。
4、三角型面积公式推导过程:取三角形ABC上AB的中点D、AC的中点E,过点A、D、E及底边BC作长方形FGHJ,则三角形ABC的面积等于长方形FGHJ的面积,即(底÷2)×高。
5、任意三角形的面积公式(海伦公式):S=√p(p-a)(p-b)(p-c),p=(a+b+c)/2,a.b.c,为三角形三边。证明:证一 勾股定理 分析:先从三角形最基本的计算公式S△ABC = aha入手,运用勾股定理推导出海伦公式。
三角型面积公式推导
1、方法二:将三角形两边中点连线并剪下一个三角形,通过平移,可以拼成一个平行四边形,可以说平行四边形和三角形高相同,底是2:1的关系,也可以说底相同,高是2:1。观察方向不同,叙述不同,但面积公式相同。
2、所以:三角形的面积=底×高÷2,即S=ah÷2。七种三角形的面积公式 已知三角形底a,高h,则等腰三角形的面积为 S=ah/2。已知三角形三边a,b,c,则 S=√p(p-a)(p-b)(p-c) [p=(a+b+c)/2]。
3、三角型面积公式推导过程:取三角形ABC上AB的中点D、AC的中点E,过点A、D、E及底边BC作长方形FGHJ,则三角形ABC的面积等于长方形FGHJ的面积,即(底÷2)×高。
4、三角形的面积计算公式为S=ah/2,(a为底、h为高)。假设一个三角形的底为6米,高为4米,那么他的面积S=(4×6)/2=12米。
5、三角形面积推导公式的过程是,将两个完全一样的三角形都可以拼成一个平行四边形,拼成的平行四边形的面积等于这两个三角形的面积。底等于三角形的底,高等于三角形的高,所以一个三角形的面积=这个平行四边形的面积的一半。

6、将这两个三角形一正一反地组成平行四边形。然后对照进行推导。
三角形的面积计算公式是怎样推导出来的
用平行四边形面积公式推导的,因为两个相同的三角形都可以组成平行四边形,平行四边形面积公式是用矩形面积公式推导的,因为任何平行四边形都可以通过切割结合变成一个矩形。
三角形的面积×2=底×高。所以:三角形的面积=底×高÷2,即S=ah÷2。七种三角形的面积公式 已知三角形底a,高h,则等腰三角形的面积为 S=ah/2。
根据公式:三角形面积=(底×高)/2 可知:底×高=2面积;底=三角形面积×2÷高;高=三角形面积×2÷底。(面积=底×高÷2。
方法一:两个完全相同的三角形可以拼成一个平行四边形,三角形的底就是平行四边形的底,高即为平行四边形的高。
三角形面积的推导过程
三角形面积公式推导有三种方法分别是平行四边形、三角形、三角形垂线。方法一:两个完全相同的三角形可以并迟敏拼成一个平行四边形,三角形的底就是平行四边形的底,高即为平行四边形的高。
三角型面积公式推导过程:取三角形ABC上AB的中点D、AC的中点E,过点A、D、E及底边BC作长方形FGHJ,则三角形ABC的面积等于长方形FGHJ的面积,即(底÷2)×高。
根据公式:三角形面积=(底×高)/2 可知:底×高=2面积;底=三角形面积×2÷高;高=三角形面积×2÷底。(面积=底×高÷2。
三角形面积的推导过程,相关内容如下:三角形的面积可以通过公式S=1/2*底边长*高得出。推导基本思路 要推导三角形的面积公式,我们需要找到一个与三角形相关的基本量,并通过合理的推导得出面积的计算公式。
三角形面积推导公式的过程是,将两个完全一样的三角形都可以拼成一个平行四边形,拼成的平行四边形的面积等于这两个三角形的面积。底等于三角形的底,高等于三角形的高,所以一个三角形的面积=这个平行四边形的面积的一半。
任意三角形的面积公式(海伦公式):S=√p(p-a)(p-b)(p-c),p=(a+b+c)/2,a.b.c,为三角形三边。证明:证一 勾股定理 分析:先从三角形最基本的计算公式S△ABC = aha入手,运用勾股定理推导出海伦公式。
到此,以上就是小编对于三角形面积推导过程用了什么思想的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏