本篇目录:
- 1、高等数学。证明(n→∞)limxn=1求具体过程
- 2、求极限,设xn=1/3+1/3^2+...+1/3^n,则当n趋向于无穷时,xn的极限是多少...
- 3、求详细过程
- 4、数列极限的证明与求解,求详细过程
- 5、帮忙解答一下,刚上高数。有点迷茫。。要过程。谢啦
高等数学。证明(n→∞)limxn=1求具体过程
单调递增会解?,limXn=1,Xn=n/n+1=1-1/n+1。limXn=lim(1-1/n+1)=lim1-lim1/n+1=1,lim1=1,lim1/n+1=0,因为当n趋于无穷大的时候时,等于0。
证:设f(x)=x+x^2+x^3+…+x^n。 因为在(0,+∞)区间,f(x)=1+2x+3x^2+…+nx^(n-1)0, 所以在(0,+∞)区间,f(x)单调递增。
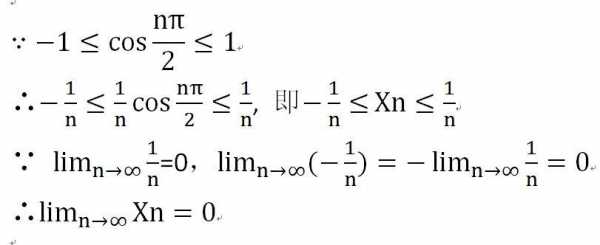
当 n=2时,0Xn+1=sinXn1,所以 有 Xn+1=sinXnXn,因此 { Xn}是单调递减的有界数列,故存在极限,设 lim(n→∞)Xn=x,则x=sinx,解得 x=0,即 lim(n→∞)Xn=0。
求极限,设xn=1/3+1/3^2+...+1/3^n,则当n趋向于无穷时,xn的极限是多少...
设{xn}为一个无穷实数数列的集合。如果存在实数a,对于任意正数ε (不论其多么小),都N0,使不等式|xn-a|ε在n∈(N,+∞)上恒成立,那么就称常数a是数列{xn} 的极限,或称数列{xn}收敛于a。记作 或。
X(2n-1)=1/(2n -1),n趋向于正无穷时,极限为0。X(2n)=[1/(2n)]+1,n趋向于正无穷时,极限为1。因为xn的两个子序列的极限不同,所以无极限。完善 极限思想的完善,与微积分的严格化的密切联系。
综述:Xn=2^n-1/3^n,当n趋近于无穷大时,就极限,两个指数函数,底数小于1,是两个值都为0,所以为0-0=0。所以答案是0。数学:数学是研究数量、结构、变化、空间以及信息等概念的一门学科。

所以任意ε0,取N=lg(1/ε)则当nN时,就有|0.999999(n个)-1|ε 即lim0.99999(n个)=1 求极限基本方法有:分式中,分子分母同除以最高次,化无穷大为无穷小计算,无穷小直接以0代入。
求详细过程
1、将废轮胎、放入负压状态的废轮胎炼油设备裂解反应釜中,催化加热,使其产生油气。废轮胎炼油的原理是热裂解。
2、x)+C.其中∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数,求已知函数不定积分的过程叫做对这个函数进行积分。
3、复数的幅角详细的过程:设z=a+bi((a、b∈R)),那么tanθ=b/a,θ为幅角。当 a不等于0时,a+ib的幅角就是arctan b/a 。当a=0时,ib的角是90°,-ib的角是-90°,b是大于0的。

4、求函数f(x)的极值:找到等式f(x)=0的根 在等式的左右检查f(x)值的符号。如果为负数,则f(x)在这个根得到最大值;如果为正数则f(x)在这个根得到最小值。判断f(x)无意义的点。
5、这样想:如下图 五个格子图 这里有五个格子,如果把它看成是1,那么1/5就表示五个格子中的一个格子。
6、(c-a)(d-a)(c-b)(d-b)(d-c),详细过程如图。
数列极限的证明与求解,求详细过程
利用定义来证明数列的极限。注意!只能利用定义来进行求取和证明,不可通过性质。检查解答过程,发现解题过程中的问题进行修改。
数列极限的证明过程如下:(1)通项公式法:数列的第N项an与项的序数n之间的关系可以用一个公式an=f(n)来表示。
数列极限证明题型及解题方法如下:在求数列n项和极限利用夹逼准则时,往往对分母进行统一化放缩,分母都取最大的,整体就放小了;分母都取最小的,整体就放大了,然后再计算两边的极限即可。
数列极限的证明题解法,利用夹逼准则或者利用单调有界准则。利用夹逼准则关键是进行不等式放缩。
帮忙解答一下,刚上高数。有点迷茫。。要过程。谢啦
1、通项的系数an=1/(n*3^n),a(n+1)/an=n/(3n+3)→1/3(n→∞),所以收敛半径R=1/(1/3)=3,收敛区间是(-3,-3)。x=3时,幂级数变为∑1/n,发散。
2、若是学工科的,只要记住公式,能用它解题就行啦!若是学理科的,那就必须掌握证明的方法。
3、以我看可以如下思考:y=arccos(sinx)cosy=sinx sin(π/2-y)=sinx 再考虑周期性和定义域等。
4、所以只需直线(m+2)x-y+m=0不过原点且不与直线x+y=0、x轴平行即可。
5、假如x等于0,则a.b.c取任意值。假如x不等于0 可将x+1代入f(x)得到等式f(x+1)-f(x)=~~~(~~~表示2的x幂乘x平方 那部分)等式两边消去2的x幂,得关于x的等式。
到此,以上就是小编对于lim xn的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏