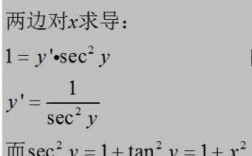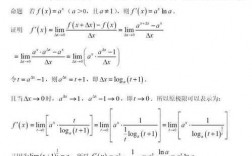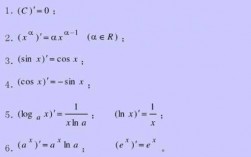本篇目录:
- 1、求导数,求解详细过程
- 2、求导怎么得到的求详细步骤
- 3、求导数。要详细过程。
- 4、求导的三个基本步骤
- 5、导数公式推导过程是什么?
求导数,求解详细过程
1、- 一次函数的导数:(ax + b) = a,其中a和b是常数。- 指数函数的导数:(e^x) = e^x,其中e是自然对数的底数。
2、需要注意的是,当y0=0时,切线方程为x=x0,即椭圆在轴上的点的切线为垂直于x轴的直线。 综上所述,对椭圆求导的过程可以分为以下几步:将椭圆的方程写成函数形式,对函数求导,利用导数公式求解切线斜率,利用切线斜率公式求解切线方程。

3、要求函数的导数,可以使用微积分中的导数定义或常用的导数规则来求解。
4、导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。
求导怎么得到的求详细步骤
- 常数函数的导数:(c) = 0,其中c是常数。- 幂函数的导数:(x^n) = n * x^(n-1),其中n是常数。- 一次函数的导数:(ax + b) = a,其中a和b是常数。
要求一个函数的导数,可以使用以下方法: 使用导数定义计算导数:根据导数的定义,函数 f(x) 在某一点 x 处的导数可以通过计算极限来求得。

求导的主要方法是利用求导公式,这些公式是通过一些基本的导数性质推导而来的。常见的求导公式包括:(x^n)=nx^(n-1),(sinx)=cosx,(cosx)=-sinx,(e^x)=e^x等。
例题:如图片所示。方程的左右两边同时求出关于x的偏导数。求出u关于x的导数,期中u为符合函数,u=f(x,y,z),x=x,y=0*x,z=(x,y)。将z关于x的导数带入u关于x的导数中。
第一步:确定函数的定义域.如本题函数的定义域为R。第二步:求f(x)的导数f′(x)。第三步:求方程f′(x)=0的根。
在数学中求导是一种重要的运算,它可以帮助我们求出函数的变化率和极值等信息。下面将详细介绍对椭圆求导的过程 首先,我们需要将椭圆的方程写成函数形式。

求导数。要详细过程。
求导过程如下:y=e^(lnx/x)*(lnx/x)=x^(1/x)*(1/x*x-lnx)/x^2=(1-lnx)x^(1/x-2)。当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。
导数公式推导过程如下:y=a^x,△y=a^(x+△x)-a^x=a^x(a^△x-1),△y/△x=a^x(a^△x-1)/△x。如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。
(1)求函数y=f(x)在x0处导数的步骤:① 求函数的增量Δy=f(x0+Δx)-f(x0)② 求平均变化率 ③ 取极限,得导数。
常函数即常数y=c(c为常数),y=0 。 幂函数y=x^n,y=n*x^(n-1)(n∈R) 。 基本导数公式3指数函数y=a^x,y=a^x * lna。 对数函数y=logaX,y=1/(xlna) (a0且a≠1,x0)。
使用导数定义求解导数的步骤主要分为三个步骤。这里以幂函数y=x^n为例说明。02 第一步,求出因变量的增量Δy=f(x+Δ)-f(x)。03 第二步,计算Δy与Δx的比值。
求导的三个基本步骤
- 常数函数的导数:(c) = 0,其中c是常数。- 幂函数的导数:(x^n) = n * x^(n-1),其中n是常数。- 一次函数的导数:(ax + b) = a,其中a和b是常数。
例题:如图片所示。方程的左右两边同时求出关于x的偏导数。求出u关于x的导数,期中u为符合函数,u=f(x,y,z),x=x,y=0*x,z=(x,y)。将z关于x的导数带入u关于x的导数中。
使用导数规则:导数有一些常用的规则可以简化计算。
操作方法 01 使用导数定义求解导数的步骤主要分为三个步骤。这里以幂函数y=x^n为例说明。02 第一步,求出因变量的增量Δy=f(x+Δ)-f(x)。03 第二步,计算Δy与Δx的比值。
Δy = (x + h)^2 - x^2 步骤二:算比值 接下来,我们将增量Δy除以对应的x的增量,得到一个比值。比值 = Δy / h 步骤三:取极限 最后一步是求极限,即让微小的x增量 h 趋向于零。这将给我们导数的定义。
导数公式推导过程是什么?
导数的基本公式的14个推导过程如下:常数函数的导数:f(x)=0,其中f(x)=c(c为常数)。解释:常数函数的导数为0,因为常数不随x的变化而变化。幂函数的导数:f(x)=ax^(a-1),其中f(x)=x^a。
导数公式推导过程如下:y=a^x,△y=a^(x+△x)-a^x=a^x(a^△x-1),△y/△x=a^x(a^△x-1)/△x。如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。
个基本导数公式推导过程如下:y=c,y=0(c为常数)。y=x^μ,y=μx^(μ-1)(μ为常数且μ≠0)。y=a^x,y=a^xlna;y=e^x,y=e^x。
复合函数求导公式推导过程有哪些 假设我们要求f(g(x))对x的导数,且f(g(x))和g(x)均可导。
到此,以上就是小编对于求导过程中的中间变量是的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏