本篇目录:
- 1、矩形有几种证法
- 2、数学:全部!写过程!矩形的判定!
- 3、矩形的判定
- 4、证明矩形所有方法大全请写出步骤和过程
- 5、怎样证明矩形(长方形)???
- 6、怎么证明矩形
矩形有几种证法
矩形的判定方法有4种。分别如下:有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。对角线相等且互相平分的四边形是矩形。矩形的介绍:有一个角是直角的平行四边形是矩形。
矩形的常见判定方法,有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
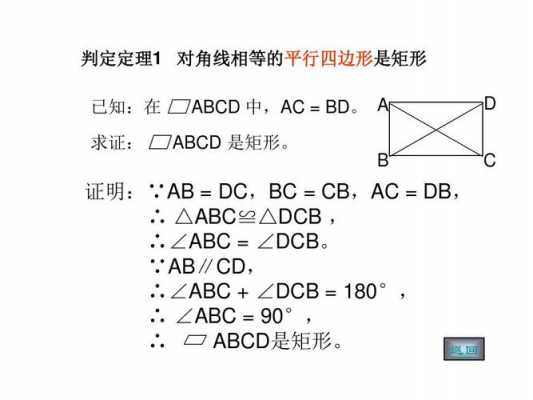
矩形的四种判定方法:有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。对角线相等且互相平分的四边形是矩形。
矩形证明方法如下:有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
①可以先证明是平行四边形,再 证明有一个角是直角。就可以确定是矩形。②先证明两条对角线相等,再证明它们互相平方。也可以确定是矩形 ③证明这个四边形有三个直角,也可以确定是矩形 常用的就是这三种方法。
证明方法:有三个角是直角的四边形是矩形;对角线互相平分且相等的四边形是矩形;有一个角为直角的平行四边形是矩形;对角线相等的平行四边形是矩形。

数学:全部!写过程!矩形的判定!
因为ABCD为平行四边形,且M为AD的中点,所以AM=MD,AB=CD。又已知MB=MC。故三角形ABM和三角形DCM全等。得出角A=角D,由平行四边形的得角A=角D=90°,故平行四边形为矩形。
矩形的判定如下:有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
正方形的判定方法:先证它是矩形,再证有一组邻边相等或对角线垂直。先证它是菱形,再证它有一个角为直角或对角线相等。
两直线平行,同旁内角互补)∴∠ABC=∠DCM=90度 ∴平行四边形ABCD是矩形(有一个内角是90度的平行四边形是矩形)第二题bd=ab+ad所以AB垂直AD。因为平行四边形ABCD。
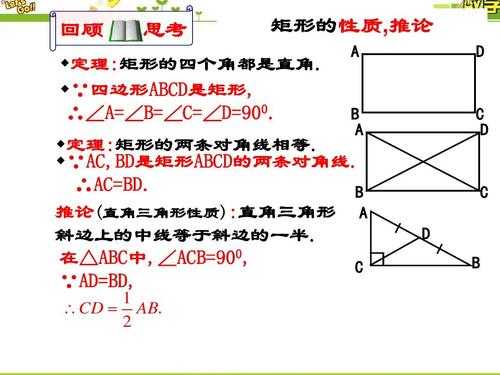
使学生经历探究矩形判定的过程,体会探索研究问题的方法,使学生在数学活动中获取成功的体验,增强自信心。
(1)求证:EO=FO(2)当点哦运动到何处时,四边形AECF是矩形?并证明你的结论。
矩形的判定
矩形的判定如下:有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
矩形的常见判定方法如下:(1)有一个角是直角的平行四边形是矩形;(2)对角线相等的平行四边形是矩形。(3)有三个角是直角的四边形是矩形。
矩形的判定有以下几点:有三个角是直角的四边形是矩形。对角线互相平分且相等的四边形是矩形。有一个角为直角的平行四边形是矩形。对角线相等的平行四边形是矩形。
证明矩形所有方法大全请写出步骤和过程
1、有三个角是直角的四边形是矩形。对角线互相平分且相等的四边形是矩形。有一个角为直角的平行四边形是矩形。对角线相等的平行四边形是矩形。
2、证明方法:有三个角是直角的四边形是矩形;对角线互相平分且相等的四边形是矩形;有一个角为直角的平行四边形是矩形;对角线相等的平行四边形是矩形。
3、有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
怎样证明矩形(长方形)???
1、有三个角是直角的四边形是长方形。对角线相等且互相平分的四边形是长方形。
2、方法一:测量四个内角的度数,如果都是直角(90度),则是长方形。这个方法基于长方形的定义,即四边都是直角。可以使用角度计等工具进行测量。
3、矩形的常见判定方法如下:(1)有一个角是直角的平行四边形是矩形。(2)对角线相等的平行四边形是矩形。(3)有三个角是直角的四边形是矩形。
4、矩形的常见判定方法如下:(1)有一个角是直角的平行四边形是矩形;(2)对角线相等的平行四边形是矩形。(3)有三个角是直角的四边形是矩形。
5、①可以先证明是平行四边形,再 证明有一个角是直角。就可以确定是矩形。②先证明两条对角线相等,再证明它们互相平方。也可以确定是矩形 ③证明这个四边形有三个直角,也可以确定是矩形 常用的就是这三种方法。
怎么证明矩形
有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
有三个角是直角的四边形是矩形。对角线互相平分且相等的四边形是矩形。有一个角为直角的平行四边形是矩形。对角线相等的平行四边形是矩形。
证明方法:有三个角是直角的四边形是矩形;对角线互相平分且相等的四边形是矩形;有一个角为直角的平行四边形是矩形;对角线相等的平行四边形是矩形。
对角线相等的平行四边形是矩形。证明某个四边形的任意三个角是直角,就可以证明这个四边形是矩形。
到此,以上就是小编对于矩形判定方法证明过程的例子的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏