本篇目录:
简述数系的五次扩充的过程
数系扩充的历史过程如下:自然数系:自然数是最基本的数学概念,从1开始,不断加1得到后续的整数。自然数包括正整数、0和负整数。在古代数学中,自然数的概念就已经开始发展,人们开始使用加减乘除等基本运算。
数系的扩充过程 ,在人类文明史的发展过程中,先有正整数Z+=N,但在Z+中减法又不封闭:35=2,不再属于Z+,为此引进新数Z和0,合成整数Z。

数系的扩充过程 ,在人类文明史的发展过程中,先有正整数Z+=N,但在Z+中减法又不封闭:35=2,不再属于Z+,为此引进新数Z和0,合成整数Z。Z=Z+∪Z∪ 0 ,这是数系的第一次扩充。
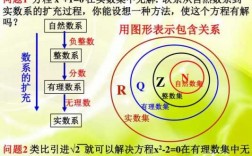
e2,en}就是扩充后的一组基。数系扩充的过程体现了数学的发展和创造的过程,也体现了数学发生、发展的客观需求.虽然学生知道自然数集、整数集、有理数集和实数集,了解它们之间的包含关系。
数系扩充的原因
1、数系扩充的原因是什么:满足数学理论的需求:数学是一门抽象的科学,它需要不断拓展和完善以适应更复杂、更广泛的实际问题。随着人们对数学理论和实际应用的深入研究,原有的数系范围可能已经无法满足需求。
2、为了解决这个问题,数学家们引入了虚数单位i,定义为i^2=-1。这样,方程的解就可以表示为±i,从而扩充了数系。
3、简述数系扩充的原因和作用如下:数系的扩充需要满足以下原则:从数系A扩充到数系B必须是AB,即A是B的真子集。
4、扩展了应用领域:数系的扩充使得数学在更多的领域得到应用。例如,负数和零的引入为代数和线性代数的发展提供了基础,使得数学在物理学、工程学、计算机科学等领域得到广泛应用。
5、从复数的引入谈数系的扩充,内容如下:复数的引入是数学史上的一个重要事件,它标志着数系的进一步扩充。在复数引入之前,数学中使用的数系是实数系,包括正数、负数和零。
6、e2,en}就是扩充后的一组基。数系扩充的过程体现了数学的发展和创造的过程,也体现了数学发生、发展的客观需求.虽然学生知道自然数集、整数集、有理数集和实数集,了解它们之间的包含关系。

数的认识教学设计
认识计数单位“百”与“千”,了解计数单位“万”,让学生建立初步的计数单位体系,掌握个、百、千、万之间的联系与区别,理解相邻两个计数单位之间的十进关系,能用知道的计数单位数出数量在万以内的数。
教学重点:让学生通过实践操作、探索、合作掌握一个十和几个一表示十几,能正确地读、写11-20各数。 教学难点:建立计数单位十的概念。
教学目标: 知识与技能目标:认识十位和个位,认识计数单位“十”和“一”,知道1120各数的组成,会正确读、写1120各数;熟练掌握1120各数的组成,能口算10加几;通过比较20以内数的大小,初步培养学生的数感。
从自然数集N扩充到实数集R经历了哪几次扩充,扩充后各加入了何种新...
符号,扩充一个范围,使得在原来范围内成立的规律,在这更大的范围内继续成立,这是数系扩充的一个特征。从自然数扩充到有理数,既满足去掉减法和除法的限制这一理论上的需要,也满足用数学来表示度量结果这一实际上的需要。
常用的数集符号:自然数集,正整数集,整数集,有理数集,实数集的表示符号分别为:自然数集即是非负整数集。
有一些特殊的集合需要记忆:非负整数集(即自然数集)N正整数集N或N+。整数集Z有理数集Q实数集R。集合的表示方法:列举法与描述法。①列举法:{a,b,c……}。②描述法:将集合中的元素的公共属性描述出来。
数的扩充
A中不是永远可行的某种运算,在B中永远可行,例如,实数系扩充为复数系后,开方的运算就永远可行,再如,自然数系扩充为整数系后,减法的运算就能实行等。
扩数是数系的扩充它是在人类认识和运用数的历史发展过程中,逐步形成的、不断扩大数的范围的一些基本原则。
最终得到一组线性无关的向量{e1,e2,es}容易看出{f1,f2,fn}能与{e1,e2,es}互相线性表示得出{e1,e2,es}的极大无关组个数为n又因为{e1,e2,es}线性无关,所以s=n所以{e1,e2,en}就是扩充后的一组基。
到此,以上就是小编对于数的扩充需要注意什么的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏