本篇目录:
- 1、如何推导海伦公式
- 2、什么是海伦公式以及他的详细证明
- 3、海伦公式如何推导?
- 4、海伦公式是怎样推导出来的
如何推导海伦公式
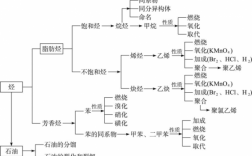
海伦定理表达式为:S=√p(p-a)(p-b)(p-c)海伦定理意义:海伦定理的提出为计算三角形和多边形的面积提供了一种新的方法和思路。
海伦——秦九韶公式如下:假设有一个三角形,边长分别为a、b、c,三角形的面积S可由以下公式求得:S=√[p(p-a)(p-b)(p-c)] ,而公式里的p为半周长:p=(a+b+c)/2 。

推导海伦公式:用勾股定理 证明: 根据勾股定理,得:此时化简得出海伦公式。
分析:先从三角形最基本的计算公式s△abc = aha入手,运用勾股定理推导出海伦公式。证明:如图ha⊥bc,根据勾股定理,得:x = y = ha = = = ∴ s△abc = aha= a× = 此时s△abc为变形④,故得证。
什么是海伦公式以及他的详细证明
1、= 就是著名的海伦公式,在希腊数学家海伦的著作《测地术》中有记载。海伦公式在解题中有十分重要的应用。
2、海伦公式又译作希伦公式、海龙公式、希罗公式、海伦-秦九韶公式。它是利用三角形的三条边的边长直接求三角形面积的公式。表达式为:S=√p(p-a)(p-b)(p-c)。

3、海伦公式就是用三角形三边长表示出三角形面积的一个公式。从三角形其中一顶点向对边作高,已知三边长,可用勾股定理列方程组表示出高,再用底乘高除以2即可证明。
4、海伦定理表达式为:S=√p(p-a)(p-b)(p-c)海伦定理意义:海伦定理的提出为计算三角形和多边形的面积提供了一种新的方法和思路。
5、这个公式是由古希腊数学家阿基米德得出的,但人们常常以古希腊的数学家海伦命名这个公式,称此公式为海伦公式,因为这个公式最早出现在海伦的著作《测地术》中,并在海伦的著作《测量仪器》和《度量数》中给出证明。
海伦公式如何推导?
1、海伦定理表达式为:S=√p(p-a)(p-b)(p-c)海伦定理意义:海伦定理的提出为计算三角形和多边形的面积提供了一种新的方法和思路。

2、推导海伦公式:用勾股定理 证明: 根据勾股定理,得:此时化简得出海伦公式。
3、海伦公式的推导过程如图:海伦公式:利用三角形的三条边的边长直接求三角形面积的公式。(a、b、c分别为三角形三条边的边长,p为三角形周长的一半)。
4、海伦公式的证明 证一 勾股定理 分析:先从三角形最基本的计算公式s△abc = aha入手,运用勾股定理推导出海伦公式。
海伦公式是怎样推导出来的
1、海伦定理表达式为:S=√p(p-a)(p-b)(p-c)海伦定理意义:海伦定理的提出为计算三角形和多边形的面积提供了一种新的方法和思路。
2、海伦——秦九韶公式如下:假设有一个三角形,边长分别为a、b、c,三角形的面积S可由以下公式求得:S=√[p(p-a)(p-b)(p-c)] ,而公式里的p为半周长:p=(a+b+c)/2 。
3、推导海伦公式:用勾股定理 证明: 根据勾股定理,得:此时化简得出海伦公式。
到此,以上就是小编对于海伦公式最简单推导的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏