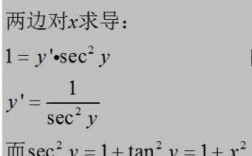本篇目录:
- 1、sin方X的求导,要过程
- 2、sin平方x怎么求导
- 3、sin方x的导数怎么求
- 4、sin平方x的导数怎么求?
- 5、sin平方x的导数
- 6、怎么对sin^x求导
sin方X的求导,要过程
1、sinx的解答过程如下:(sinx)=2sinx*(sinx)=2sinxcosx =sin(2x)sinx是一个由u=sinx和u复合的复合函数。复合函数,是指以一个函数作为另一个函数的自变量。
2、sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。

3、运算方法有以下两种:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。(sinx)=[(1-cos2x)/2]=[1/2-(cos2x)/2]=0-(-sin2x)(2x)=(sin2x)×2=sin2x。
4、sin的平方x求导如下:sin平万x来导属于复合函数的求导,并且某求导可分为一阶求导、二阶求导和高阶求导。
5、运算方法有以下两种:(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。
sin平方x怎么求导
sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
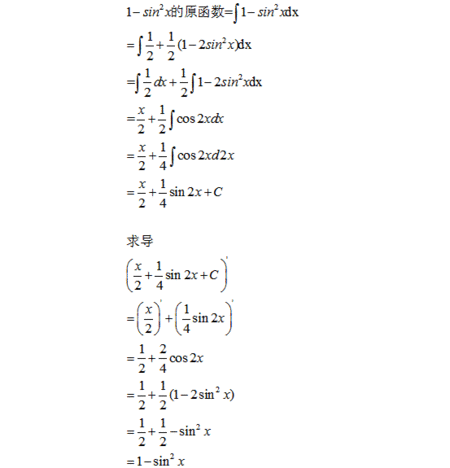
运算方法有以下两种:(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。
运算方法有以下两种:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。(sinx)=[(1-cos2x)/2]=[1/2-(cos2x)/2]=0-(-sin2x)(2x)=(sin2x)×2=sin2x。
若h(a)=f(g(x)),则h(a)=f(g(x))g(x)。
sinx的平方求导如下:先求外函数y=(sinx),再求内函数sinx的导数,即cosx。故(sinx)的导数为2sinxcos,也就是sin2x。

被称为幂指函数,在经济活动中会大量涉及此类函数,注意到它很特别。既不是指数函数又不是幂函数,它的幂底和指数上都有自变量x,所以不能用初等函数的微分法处理了。这里介绍一个专门解决此类函数的方法,对数求导法。
sin方x的导数怎么求
sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
运算方法有以下两种:(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。
运算方法有以下两种:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。(sinx)=[(1-cos2x)/2]=[1/2-(cos2x)/2]=0-(-sin2x)(2x)=(sin2x)×2=sin2x。
sin平方x的导数怎么求?
1、sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
2、运算方法有以下两种:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。(sinx)=[(1-cos2x)/2]=[1/2-(cos2x)/2]=0-(-sin2x)(2x)=(sin2x)×2=sin2x。
3、运算方法有以下两种:(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。
4、若h(a)=f(g(x)),则h(a)=f(g(x))g(x)。
5、sinx= =(1-cos2x)/2 根据降幂公式:sinα=[1-cos(2α)]/2,得出以上结论。
6、sinx的平方的导数是sin2x。先求外函数y=(sinx)2,再求内函数sinx的导数,即cosx。故(sinx)2的导数为2sinxcos,也就是sin2x。
sin平方x的导数
1、(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。(sinx) = [(1-cos2x)/2] = [1/2 - (cos2x)/2] = 0 - (-sin2x)(2x) = (sin2x)×2 = sin2x。
2、sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
3、sin2x的导数是cos(2x) * 2。sin2x的导数可以通过求导公式进行计算。根据三角函数的求导规则,对于函数f(x) = sin(ax),其导数为f(x) = acos(ax)。
怎么对sin^x求导
1、运算方法有以下两种:(sinx) = 2sinx(sinx) = 2sinxcosx = sin2x。
2、sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
3、但y=[(sinx)^x为复合函数,sinx不是常数,不能套用上面的公式进行求导,∴y′=[(sinx)^x ln(sinx)](sinx)′=cos x[(sinx)^x ln(sinx)]的做法不对。
4、因为是复合函数,所以用复合函数求导法则。外层函数是sint,内层函数是t=x。导数是对x求的,所以y先对t求导,就是cost,然后t对x求导,就是2x,再把t换成x。答案就是cosx×2x。
5、/3!)(sinx)^3+(1/5!)(sinx)^5-(1/7!)(sinx)^7……sin(sinx)∽x,设sinx=t,则sint~t,所以sint~t~sinx~x,由等价无穷小的传递性,也可以直接算,求五次导数,可以解出除了x项以外都是0。
到此,以上就是小编对于的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏