本篇目录：

• 1、椭圆公式的推导过程是什么?
• 2、椭圆的极坐标方程的推导过程是什么?
• 3、椭圆参数方程的推导过程
• 4、如何用椭圆算出点的坐标?

椭圆公式的推导过程是什么?

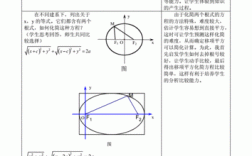
推导过程：离心率e=c/a，其中c是焦点到椭圆中心的距离，a是椭圆的长半轴长度。可以根据椭圆的定义来推导这个公式。椭圆是平面上到两个固定点F1和F2的距离之和等于常数（大于｜F1F2|）的点的轨迹。

椭圆方程推导过程如下：假设给定点的坐标为 (x0， y0)，椭圆的标准方程为 ((x-h)^2)/a^2 + ((y-k)^2)/b^2 = 1，其中 (h， k) 是椭圆的中心坐燃逗并标，a 和 b 分别是椭圆的长半轴和短半轴。

推导：PF1+PF2F1F2(P为椭圆上的点，F为焦点)平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。

椭圆周长公式：L=2πb+4(a-b)根据椭圆第一定义，用a表示椭圆长半轴的长，b表示椭圆短半轴的长，且ab0。

椭圆的极坐标方程的推导过程是什么?

椭圆的极坐标方程是从椭圆的标准坐标方程推出来的。

参数方程 x=acosθ，y=bsinθ。

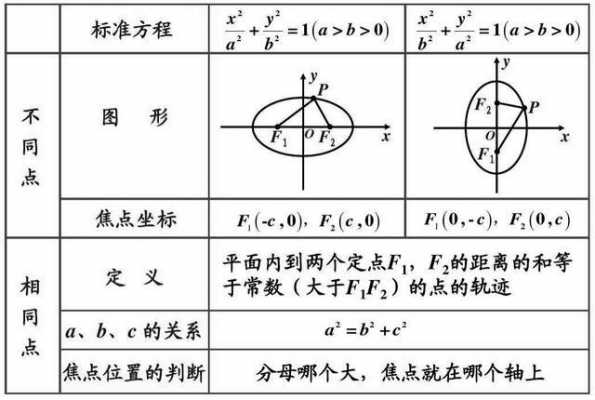
椭圆是一个几何图形，具有两个焦点和一个长轴和短轴。椭圆的极坐标方程描述了从原点出发的射线与椭圆相交的点的极坐标坐标。在椭圆的极坐标方程中，离心率ε是一个非负实数，表示椭圆的形状。

椭圆的极坐标方程公式：r=a(1-e)/(1-ecosθ)。在数学中，极坐标系是一个二维坐标系统。该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。

椭圆极坐标方程：p=ep/(1-ec0sθ)。椭圆 椭圆是把平面内与两个定点的距的和等于常数(大于)的点的轨迹叫做椭园.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。

椭圆参数方程的推导过程

1、椭圆的参数方程推导过程：(1)的平方加(2)的平方 化简得：证明：将任意一点P的坐标（Rsinθ-c，Rcosθ)代入方程 = 说明P点是椭圆标准方程上的一点。

2、随圆的参数方程推导过程是（2a-R）cosp=2c-Rsin0。（2a-R）sinq=Rcos0。椭圆参数方程是以焦点（c，0）为圆心，R为变半径的曲线方程。

3、把标准椭圆的参数方程 旋转 θ 角，再平移到 ，得到的参数方程为：解出：由 可得：形如 的二次曲线方程可以写成矩阵形式：其中 ，称作(x，y)的齐次坐标， 为系数矩阵。

4、再用ab除两边，即得焦点在y轴上的椭圆的标准方程为：y/a+x/b=1，其中a-b=c；ab.其中a为长半轴之长，b为短半轴之长，c为半焦距。

5、RX/a）^2+(RY/b)^2-R^2=0 再把等式改写X^2/a^2+Y^2/b^2=1。

如何用椭圆算出点的坐标?

1、椭球面上表示点的坐标的方法有：本质上和球面坐标是一样的，先伸缩变换，然后计算雅各比行列式。标准方程是在笛卡尔（直角）坐标系下的方程，而参数方程是在球坐标系下的椭圆方程。

2、椭圆焦点坐标公式是a^2-b^2=c^2，其中a为长轴长，b为短轴长，c为焦距。如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。

3、椭圆的顶点坐标公式x^2/a^2+y^2/b^2=1。椭圆是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。

4、x=acost；y=bsint；是长半轴为a，短半轴为b，焦点在x轴上的椭圆方程。

5、a 短半轴：b 椭圆中心：o 椭圆上的任一点p(x，y)：给定一个x的坐标，有两个y与之对应：｛x，y=±b√(1-x/a)｝ （1）其中：x∈[-a，a](1)就是椭圆上的任一点p(x，y)的坐标。

6、假设椭圆方程为(x/a)^2+(y/b)^2=c 那么任意一个椭圆上点的坐标为(x，y)其中x=±b*sqrt(c-(x/a)^2)注：sqrt表示开根号的意思；^2表示平方的意思。

到此，以上就是小编对于椭圆的坐标系的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。