本篇目录:
1/cosx不定积分的公式推导过程
1、/cosx的不定积分是:ln|(secx+tanx)|+c。证明为 ∫1/cosxdx=∫secxdx=∫(secx+secxtanx)/(secx+tanx)dx=∫1/(secx+tanx)d(secx+tanx)=ln|(secx+tanx)|+c。
2、计算过程:∫1/cosxdx=∫secxdx=∫(secx+secxtanx)/(secx+tanx) dx=∫1/(secx+tanx) d(secx+tanx) =ln|(secx+tanx) |+c。

3、=1/2[ln(1+sinx)-ln(1-sinx)]+C。=1/2ln[(1+sinx)/(1-sinx)]+C。相关信息:函数的积分表示了函数在某个区域上的整体性质,改变函数某点的取值不会改变它的积分值。
这个重要的反常积分的计算过程
计算反常积分公式:I^2=[∫e^(-x^2)dx]。反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。
反常积分常用公式是I=(0,∝)∫[e^(-x^2)]dx。定积分的积分区间都是有限的,被积函数都是有界的。
在求导后自变量的值为负时,在导数后加“”,这种情况称为反常积分。当自变量的值为负时,原函数在(0,+∞)内有反常性质了即求导后自变量值变为非负数时,则原函数与之有解。
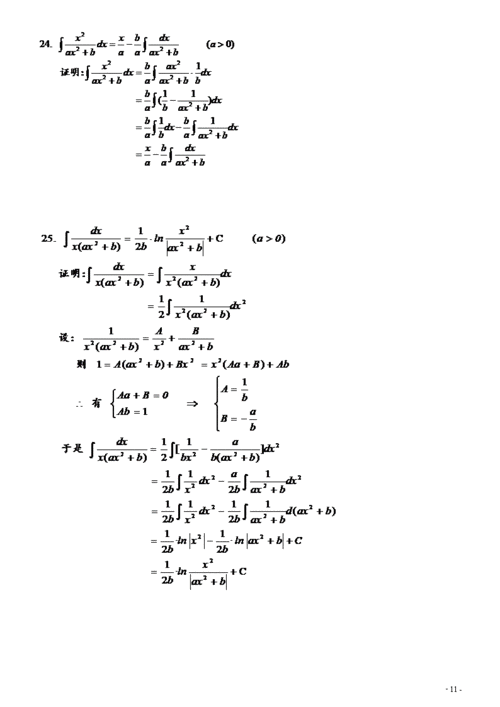
反常积分四个常用公式如图所示:定积分的积分区间都是有限的,被积函数都是有界的。但在实际应用和理论研究中,还会遇到一些在无限区间上定义的函数或有限区间上的无界函数,对它们也需要考虑类似于定积分的问题。
反常积分计算的方法有:定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。定理2:设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
怎么求定积分的值,要详细步骤谢谢
1、计算过程如下:一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分。
2、定积分是把函数在某个区间上的图象[a,b]分成n份,用平行于y轴的直线把其分割成无数个矩形,再求当n→+∞时所有这些矩形面积的和。

3、定积分定义:设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子区间[x0,x1], (x1,x2], (x2,x3], …, (xn-1,xn],其中x0=a,xn=b。
定积分的公式怎么推导的呢?
定积分求导可以通过定积分求导公式[∫(a,c)f(x)dx]=0来实现。定积分求导可以通过定积分求导公式来实现,具体题目再具体分析,定积分求导公式为:[∫(a,c)f(x)dx]=0。
∫xcosxdx =∫xdsinx =xsinx-∫sinxdx =xsinx+cosx+C 。定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。一个函数可以存在不定积分,而不存在定积分,也可以存在定积分,而不存在不定积分。
估值定理的推导,可以直接用 f(x)-m的积分≥0来证明,M的情形类似。
积分计算公式是什么?
1、基本公式:∫e^xdx=e^x+C;根据这一基本公式带入x的值即可算出积分。
2、以下是24个常见的基本积分公式: ∫k dx = kx + C,其中k为常数,C为常数,x为自变量。 ∫x^n dx = (x^(n+1))/(n+1) + C,其中n为非负整数,C为常数。
3、基本积分公式如下:牛顿-莱布尼茨公式,又称为微积分基本公式。格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分。
4、个基本积分公式:∫kdx=kx+C(k是常数)。∫x^udx=(x^u+1)/(u+1)+c。∫1/xdx=ln|x|+c。∫dx=arctanx+C21+x1。∫dx=arcsinx+C21x。
到此,以上就是小编对于积分的公式推导的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏