电路的建模过程（建立电路的模型会不会对电路的计算带来大的误差?）-义乌市趣迅电子商务商行

本篇目录：

数学建模的步骤：模型准备：了解问题的实际背景，明确建模目的，搜集必需的各种信息，尽量弄清对象的特征。模型假设：根据对象的特征和建模目的，对问题进行必要的、合理的简化，用精确的语言作出假设。

逻辑方法：是数学理论研究的重要方法，对社会学和经济学等领域的实际问题，在决策，对策等学科中得到广泛应用。常微分方程：解决两个变量之间的变化规律，关键是建立“瞬时变化率”的表达式。

数学建模五个步骤顺序如下：第一步：根据研究对象的特点，确定研究对象属哪类自然事物或自然现象，从而确定使用何种数学方法与建立何种数学模型。

数学建模的一般步骤如下：实际问题通过抽象、简化、假设，确定变量、参数。建立数学模型并数学、数值地求解、确定参数。用实际问题的实测数据等来检验该数学模型。

初中生的数学建模活动包含步骤如下：理解问题：首先，你需要明确和理解实际问题的本质。这需要你具有对问题的敏感性和对数学概念的理解。抽象和简化问题：接着，你需要将实际问题抽象成数学问题。

数学建模就是利用数学模型来解决问题。提炼数学模型，就是运用科学抽象法，把复杂的研究对象转化为数学问题，经合理简化后，建立起揭示研究对象定量的规律性的数学关系式。

数学建模的过程包括：模型准备、模型假设、模型建立、模型求解、模型的分析与检验、模型应用。

合理假设作出合理假设，是建模的一个关键步骤。一个实际问题不经简化、假设，很难直接翻译成数学问题，即使可能也会因其过于复杂而难以求解。因此，根据对象的特征和建模的目的，需要对问题进行必要合理地简化。

比例分析法：建立变量之间函数关系的最基本最常用的方法。代数方法：求解离散问题（离散的数据、符号、图形）的主要方法。

数学建模是指将实际问题抽象成数学模型，并通过对模型的分析和计算来解决实际问题的过程。它是现代科学和工程领域中广泛应用的一种方法，也是解决复杂问题的重要手段之一。

建模方法很多，随着具体对象系统的特性、复杂程度、用途不同而异。通常多采用物理模拟和数学模拟方法，现已发展到功能模拟和智能模拟方法。

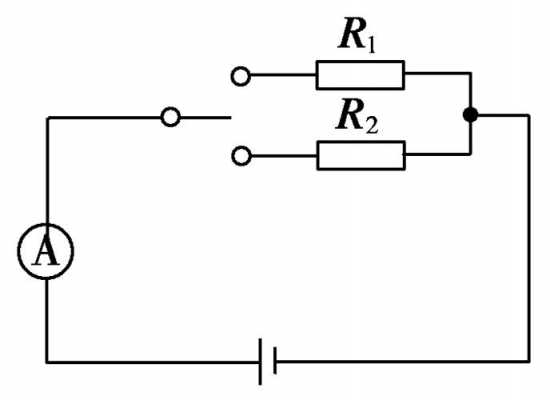
伸缩翻转法在实验室接电路时常常可以这样操作，无阻导线可以延长或缩短，也可以翻过来转过去，或将一支路翻到别处，翻转时支路的两端保持不动；导线也可以从其所在节点上沿其它导线滑动，但不能越过元件。

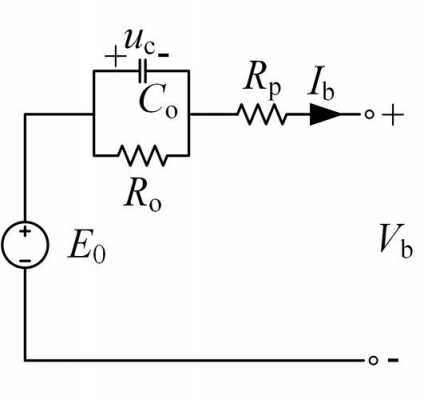
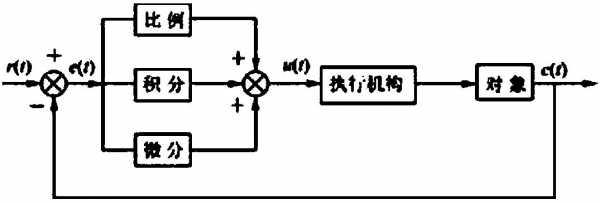
．交流等效电路分析法。首先画出交流等效电路，再分析电路的交流状态，即：电路有信号输入时，电路中各环节的电压和电流是否按输入信号的规律变化、是放大、振荡，还是限幅削波、整形、鉴相等；2．直流等效电路分析法。

组合逻辑电路的分析流程与逻辑表示只有在决定事物结果的全部条件具备时，结果才发生。

到此，以上就是小编对于建立电路的模型会不会对电路的计算带来大的误差?的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。