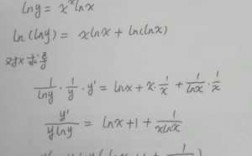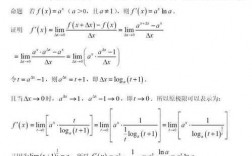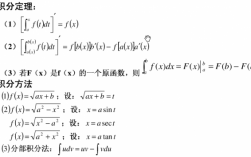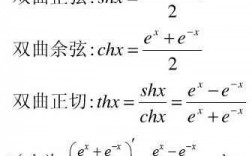本篇目录:
- 1、正切函数的导数怎么求?
- 2、导数公式推导过程是怎么样的?
- 3、如何用导数求正切函数?
- 4、tanx的导数怎么求?
- 5、正切函数求导
- 6、正切函数导数怎么求
正切函数的导数怎么求?
1、+tan^2 x=sec^2 x。证明过程如下:(1)tan x = sin x/cos x;(2)sec x =1/cos x;(3)tan^2 x=sin^2 x/cos^2 x;(4)1+tan^2 x=1+sin^2 x/cos^2 x=sec^2 x。
2、+(cotx)^2=(cscx)^2。倒数关系:sinxcscx=1,cosx.secx=1,tanxcotx=1。

3、其具体过程是:(tanx)′=(sinx/cosx)′=[(sinx)′cosx-sinx·(cosx)′]/cos^2x=[cos^2x+sin^2x]/cos^2x=1/cos^2x=sec^2x。即tanx求导结果为sec^2x。
4、tan的加法公式:tan(a+b) = (tana+tanb)/(1-tana tanb)。在Rt△ABC(直角三角形)中,∠C=90°,AB是∠来C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数tanB=b/a。
5、正切求导公式是(tanx)=secx*secx。求导是数学计算中的一个计算方法,它的定义就是,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。
导数公式推导过程是怎么样的?
1、导数的基本公式的14个推导过程如下:常数函数的导数:f(x)=0,其中f(x)=c(c为常数)。解释:常数函数的导数为0,因为常数不随x的变化而变化。幂函数的导数:f(x)=ax^(a-1),其中f(x)=x^a。
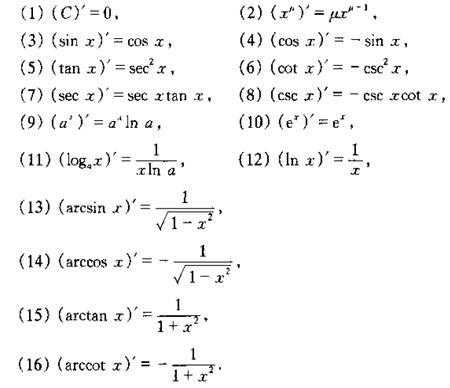
2、导数公式推导过程如下:y=a^x,△y=a^(x+△x)-a^x=a^x(a^△x-1),△y/△x=a^x(a^△x-1)/△x。如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。
3、个基本导数公式推导过程如下:y=c,y=0(c为常数)。y=x^μ,y=μx^(μ-1)(μ为常数且μ≠0)。y=a^x,y=a^xlna;y=e^x,y=e^x。
4、导数公式推导过程几个常见的公式 (链式法则)y=f[g(x)],y=f[g(x)]·g(x) ,f[g(x)]中g(x) 看作整个变量,而g(x) 中把x看作变量。y=u*v,y=uv+uv(一般的leibniz公式)。
5、常见高阶导数8个公式是:y=c,y=0(c为常数) 。y=x^μ,y=μx^(μ-1)(μ为常数且μ≠0)。y=a^x,y=a^x lna;y=e^x,y=e^x。

如何用导数求正切函数?
1、基本公式:tanx+1=secx。解答过程如下:tanx=sinx/cosx。
2、解答过程如下:=∫secxd(tanx)=secxtanx-∫tanxd(secx)=secxtanx-∫secx(tanx)^2dx =secxtanx-∫(secx)^3dx+∫secxdx =secxtanx-I+ln|secx+tanx| I=(1/2)×(secxtanx+ln|secx+tanx|)+C。
3、+tan^2 x=sec^2 x。证明过程如下:(1)tan x = sin x/cos x;(2)sec x =1/cos x;(3)tan^2 x=sin^2 x/cos^2 x;(4)1+tan^2 x=1+sin^2 x/cos^2 x=sec^2 x。
tanx的导数怎么求?
tan的导数是sec^2x。可以将tanx转化成sinx/cosx来上下推导,tanx=sinx/cosx,那么用除法求导法则来求导(f/g)′=(f′g-g′f)/g^2,即上导乘下减上乘下导,除以下的平方,tanx的导数求导套用除法求导法则就能求解。
tanx的导数:secx。求导的定义:当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。(tanx)=1/cosx=secx=1+tanx。
一般情况下,tanx的导数是需要直接记住的,即:(tanx)=(secx)^如果确实需要计算其导数,则可以通过函数导数的定义来计算tanx的导数。
tanx的导数为secx,secx的导数为tanxsecx。tanx=sinx/cosx,secx=1/cosx,secx-1= tanx。
正切函数求导
tan中文的叫法是正切,该名称属于三角函数,tan的导数是sec^2x。
【注】因为正割和余弦互为倒数,即secx=1/(cosx),所以,有时也把正切函数的导数公式写作:(tanx)=(secx)^2。正切函数的性质 定义域:{x|baix≠(π/2) kπ,k∈Z}。du 值域:实数集R。
正割函数:(secx)=tanx·secx正割求导=正割x正切。余割函数:(cscx)=-cotx·cscx余割求导=余割x余切。反正弦函数:(arcsinx)=1/√(1-x^2)。反余弦函数:(arccosx)=-1/√(1-x^2)。
正切函数导数怎么求
1、其具体过程是:(tanx)′=(sinx/cosx)′=[(sinx)′cosx-sinx·(cosx)′]/cos^2x=[cos^2x+sin^2x]/cos^2x=1/cos^2x=sec^2x。即tanx求导结果为sec^2x。
2、+tan^2 x=sec^2 x。证明过程如下:(1)tan x = sin x/cos x;(2)sec x =1/cos x;(3)tan^2 x=sin^2 x/cos^2 x;(4)1+tan^2 x=1+sin^2 x/cos^2 x=sec^2 x。
3、正切函数的导数,等于对应的余弦函数的平方的倒数(或“正割函数的平方”),即(tanx)=1/(cosx)^2(或“(tanx)=(secx)^2”)。
4、]/cosx*cos x =[cos x*cos x-(-sin x*sin x)]/cos x*cos x =1/cos x*cos x =sec x*sec x 扩展资料 不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。
5、/Cosx=Sec x,Sec x是正割函数。
到此,以上就是小编对于正切求导公式推导的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏