本篇目录:
复式格子怎么取布拉菲格子
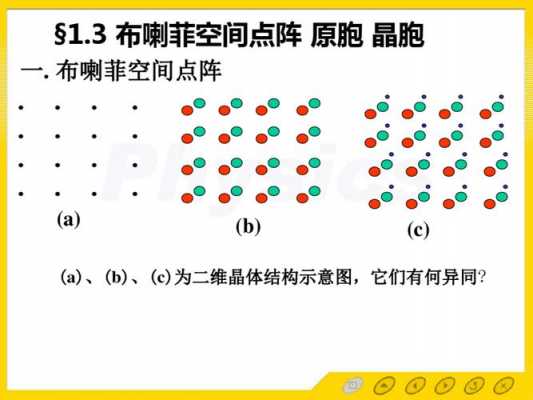
在布拉菲格子中,选定四个格点O,A,B,C并且使得矢量OA,OB,OC恰好构成三个基矢。对于某一晶面族的而言,按照晶面族的定义。
不是。如果晶体基元中包含两种或两种以上的原子,则不同的原子各自构成自身的布喇菲格子,称为子晶格,若干个相同的子晶格相互位移套构而形成所谓的复式格子。复式格子又名复式晶格。
金刚石是复式格子,和闪锌矿结构一样,金刚石是两个面心立方的简单格子沿对角线平移四分之一穿插而成,最小基元就是一个碳原子和周围连接的四个原子组成的。
晶体的布拉维格子可以通过等同点的方式确定,所谓等同点就是元素相同,周围环境也相同(符合平移对称性)的一套原子,将点阵点放在一套等同点上,根据规则(对称性最高)和体积最小划出其布拉维格子。
为什么布拉菲格子只有十四种
1、布拉菲点阵只有十四种的原因是:1848年法国晶体学家布拉菲(Bravais)证实了7种晶系中共可以有14种点阵,这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
2、对称性不对的 比如立方由于有四个三次轴的限制,不可能有C心。同样的,除了三斜,你不可能在平行六面体里随便找个位置加个点,这会破坏对称性。三斜随便找个位置加个点后面讨论。

3、Bravais晶格按照定义,经过适当平移后都不会改变,所以平移是一种对称操作。有些晶格有更强的对称性,比如镜像,旋转等。这些晶格的对称群就更大。两个晶格的对称群如果同构,他们就有相同的对称性,可以认为他们是一类的。
4、平行六面体是空间格子的最小重复单位,完整反映了晶体结构中质点的排列规律。经布拉维父子研究证明,所有空间格子中只存在十四种不同的平行六面体。所以,后来者习惯将这十四种平行六面体叫做十四种布拉维格子,也叫空间格子。
5、这样,经梳理后最终所能得到且本质上不同的空间格子类型总共只有14种,如表1和图6(见108页)所列。
谁能具体回答一下什么是布拉维点阵
Bravais lattice 布拉伐格子 在晶体中,由格矢量Rn = n1a1+n2a2+n3a3 的全部端点(格点)的集合 (ni为0和正负整数) 即构成一个空间格子,它反映了晶格的周期性。
它们代表了结点在作三维周期性平移重复排列时所仅可能有的14种基本方式,系由布拉维于1848年所最终确定并因而被称为布拉维格子(Bravais lattices,亦译“布喇菲点阵”)。
布拉维晶格在三维平面上有七大晶系,14种晶格分别为三斜晶系、单斜晶系、正交晶系、四方晶系、立方晶系、三方晶系、六角晶系。
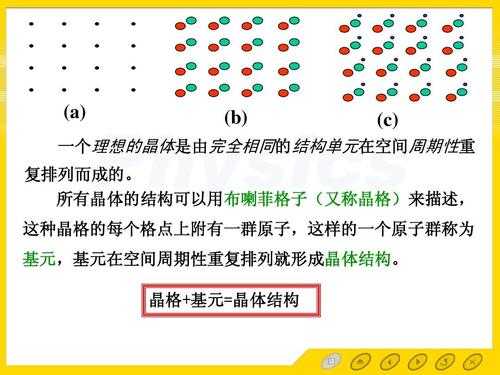
布拉菲点阵,即布拉菲格子,用位于基元平衡位置的几何点替代每一个基元,结果得到一个与晶体几何特征相同、但无任何物理实质的几何图形。处于基元平衡位置的几何点被称为格点(Lattice site)。
材料的晶体结构(若干问题)
1、布拉菲点阵不包含密排六方点阵。因为密排六方点阵不是最简单的,可以分解为其他简单的点阵。面心四方点阵可以分解为简单正交点阵。如何画出已知指数的晶向?有哪些技巧?举例说明。
2、)一般具有规则的外形,但晶体的外形不一定都是规则的,这与晶体形成的条件有关,如果条件不具备,其外形也变得不规则。所以不能仅从外观来判断,而应从其内部粒子排列情况来确定是不是晶体。2)在固定的溶点。
3、实际金属的晶体结构有哪些缺陷如下:点缺陷:空位缺陷:在晶格中缺少一个或多个原子位置的点缺陷。这种缺陷使得晶体的密度降低,通常表现为材料的导电性增加。替代缺陷:发生在晶体中某些原子被其他原子替代的情况。
4、常见的半导体的晶体结构有金刚石型、闪锌矿型、纤锌矿型和氯化钠型4种,如图和表所示。在三元化合物半导体中有部分呈黄铜矿型结构,金刚石型、闪锌矿型和氯化钠型结构可看成是由两套面心立方格子套构而成。
5、金属的实际晶体结构多晶体结构。实际使用的金属材料,绝大部分并非理想的单晶体,而是由许多小晶体(晶粒)组成的多晶体。金属的实际晶体结构存在晶体缺陷。存在点缺陷、线缺陷与面缺陷。
推导正交,四方和立方晶系的晶面间距
1、即7个晶系。按照每个阵点的周围环境相同的要求,布拉菲(Bravais A.)用数学方法推导出能够反映空间点阵全部特征的单位平面六面体只有14种,这14种空间点阵也称布拉菲点阵。
2、晶面间距的计算公式答案如下:正交晶系1/d2=h2/a2+k2/b2+l2/c2;单斜晶系1/d2={h2/a2+k2sin2β/b2+l2/c2-2hlcosβ /(ac)}/sin2β;立方晶系d=a/(h2+k2+l2)。
3、晶面间距计算公式如下:正交晶系:1/d=h/a+k/b+l/c。单斜晶系:1/d2={h2/a2+k2sin 2β/b2+l2/c2-2hlcos β/(ac)}/ sin2β 2立方晶系。d=a/(h+k+l)222。
4、面心立方晶面间距计算公式:正交晶系:1/d=h/a+k/b+l/c。单斜晶系:1/d2={h/a+ksin2β/b+l/c-2hlcosβ/(ac)}/sin2β。
到此,以上就是小编对于布拉菲点阵的结构特征的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏