borel域随机过程（随机领域）-义乌市趣迅电子商务商行

本篇目录：

Borel域，Borel 域是概率统计中最常见的一类σ代数，其定义如下：B =σ ({(∞，a]： a∈R})。

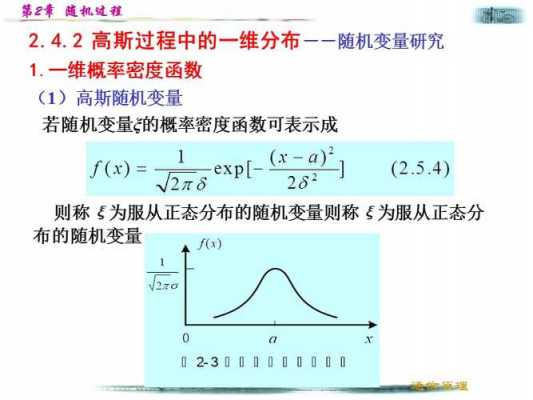
，1]内的实数。随机变量：它的自变量是什么？是样本点！样本点是什么？样本点是基本事件，就是不可再分的随机事件。它的定义域是样本空间。它的值域呢，也是实数，不过范围所有实数。

Borel手表即依波路表，一个拥有150多年的传统瑞士名表世家。从1860年borel（依波路）公司向乌拉圭出口了第一批钟表，到今天瑞士borel手表广销全球各地，在世界名表中声名赫赫。

borel手表全称是Borel and Courvoisier，译为依波路手表。瑞士依波路表1856年诞生于钟表王国瑞士的西部城市纳沙泰尔，迄今已有一百六十多年历史。依波路始终坚守着对优雅设计的不懈追求，成就经典传奇。

随机变量（random variable）表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关，都可以数量化，即都能用数量化的方式表达。它分为两种类型，离散型和连续型。

随机变量是表示随机现象各种结果的变量。例如某一时间内地铁站的人流数量，一台机器在一定时间内出现错误的次数等等，都是随机变量的实例。在做实验时，常常是相对于试验结果本身而言，我们主要还是对结果的某些函数感兴趣。

随机变量的解释概率论的基本概念。描述随机现象某一侧面的数量。如同一台机器生产一种规格的螺钉，其直径大小就是一个随机变量。随机变量分为离散型和连续型两类。

）或（6，1）。我们关注的这些量，或者更形式的说，这些定义在样本空间上的实值函数，称为随机变量。因为随机变量的值是由试验结果决定的，所以我们可以给随机变量的可能值指定概率。

可见，可选可测性是比循序可测性更强的一种可测性。进一步，使一切样本函数连续的适应过程都可测的T ×Ω上的最小σ域，称为可料σ域，关于可料σ域可测的过程称为可料过程。这又是一种比可选可测性更强的可测性。

根据测量的功能不同，测量可分为检验性测量与研究性测量2类。测量按测量方式分类可分为：直接测量、间接测量、接触测量、非接触测量、组合测量、比较测量。

可测函数列的四种收敛性是指一致收敛、几乎处处收敛、依测度收敛和几乎一致收敛。一致收敛一致收敛是可测函数列的一种收敛方式，它要求函数列的每一项都在整个定义域上无限接近于极限函数。

解释：高深的程度无法揣测。形容使人难以理解。出处：宋·高似孙《讳略》引《物类相感志》：“东海之外荒；海中有山；焦炎而峙；高深莫测。”白话释义：东海以外荒；海中有一座山；焦炎而对峙；高深不可测。

物理量一般可视为可测量，如长度、温度、时间等。可数量是不能通过测量得到的量，也称为统计量。物理量指的是什么：物理学中量度物体属性或描述物体运动状态及其变化过程的量.通俗地说，就是描述物理属性和物理现象的量。

到此，以上就是小编对于随机领域的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。