本篇目录:
- 1、幂函数公式是什么?
- 2、高中数学:幂函数最新教案
- 3、幂级数和函数的求法与步骤
- 4、关于幂函数的教案范文
幂函数公式是什么?
1、幂函数公式如下:同底数幂的乘法: a^m×a^n=a^(m+n))(m、n都是整数)。幂的乘方(a^m)^n=a^(mn),与积的乘方(ab)^n=a^nb^n。
2、同底数幂相乘:a^m·a^n=a^(m+n)。幂的乘方:(a^m)n=a^mn。积的乘方:(ab)^m=a^m·b^m。同底数幂相除:a^m÷a^n=a^(m-n)(a≠0)。a^(m+n)=a^m·a^n。
3、幂函数是一种形如 f(x) = a^x 的函数,其中 a 是常数,x 是自变量,f(x) 是因变量。幂函数的公式可以表示为:f(x) = a^x 其中,a 表示底数,x 表示指数。
4、幂函数公式很多人还不知道,现在让我们一起来看看吧! 幂函数的一般形式为:y=x a,其中a可以是任意常数。 同底数幂的乘法:a m a n=a (m n)) (m和n都是整数)。
5、幂函数的一般形式是:y=x^a,其中,a可为任何常数。 同底数幂的乘法:a^m×a^n=a^(m+n))(m、n都是整数)。 幂的乘方(a^m)^n=a^(mn),与积的乘方(ab)^n=a^nb^n。
6、对数函数计算公式:y=log(a)X,(其中a是常数,a0且a不等于1),它实际上就是指数函数的反函数,可表示为x=a^y。指数函数计算公式:一般形式为y=a^x(a0且≠1) (x∈R)。

高中数学:幂函数最新教案
本节课内容教材共分两课时进行,这是第一课时,该课时主要学习函数的单调性的的概念,依据函数图象判断函数的单调性和应用定义证明函数的单调性。
幂函数教案幂函数的共同特征(1)都是以自变量x为底数; (2)指数为常数;(3)自变量x前的系数为1; (4)只有一项。
高一数学幂函数知识点总结篇一 一次函数定义与定义式: 自变量x和因变量y有如下关系: y=kx+b 则此时称y是x的一次函数。 特别地,当b=0时,y是x的正比例函数。
高中数学数列教案设计 教材分析 (一)地位与作用 数列是高中数学重要内容之一,它不仅有着广泛的实际应用,而且起着承前启后的作用。

幂级数和函数的求法与步骤
1、求幂级数的和函数的方法,通常是:或者先定积分后求导,或先求导后定积分,或求导定积分多次联合并用;运用公比小于1的无穷等比数列求和公式。需要注意的是:运用定积分时,要特别注意积分的下限,否则将一定出错。
2、用等比级数公式,S=a1[1-q^(n+1)]/(1-q),令q=x,a1=然后当x1时,令n→∞,得S=1/(1-x)。求幂级数的和函数是一类难度较高、技巧性较强的问题。
3、求和 首先,需要将给定的幂级数的前n项进行求和,从而可以得到一个初始的函数f(x),其中的x是自变量。
4、幂级数和函数的求法有观察法、微分法、间接法。观察法:观察法是求幂级数和函数最常用的方法之一。通过观察幂级数的形式,我们可以初步判断出它的和函数。
5、常用函数展开成的幂级数,如e的x次方,1/1+x,sinx,cosx等,将要求的幂级数向熟悉的几个形式转换,一般答案是几个常用和函数的变形或组合。
关于幂函数的教案范文
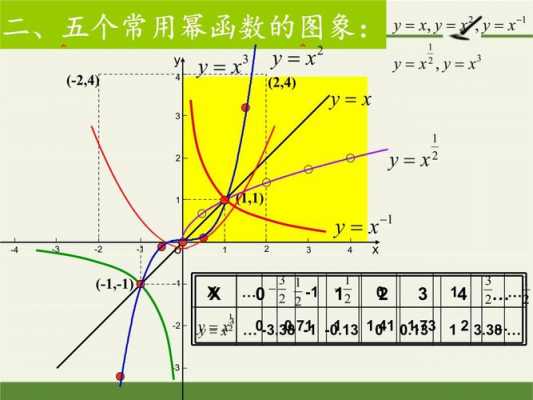
关于幂函数的教案范文一 教学任务分析: (1)理解幂函数的概念,会画五种常见幂函数的图像; (2)结合幂函数的图像,理解幂函数图像的变化情况和性质; (3)通过观察、 总结 幂函数的性质,培养学生概括抽象和识图能力。
幂函数教案幂函数的共同特征(1)都是以自变量x为底数; (2)指数为常数;(3)自变量x前的系数为1; (4)只有一项。
(1)了解并区分增函数,减函数,单调性,单调区间,奇函数,偶函数等概念。(2)能从数和形两个角度熟悉单调性和奇偶性。
到此,以上就是小编对于幂函数举例教学视频的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏