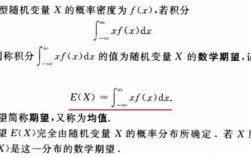本篇目录:
什么是随机过程
1、从信号分析的角度来说,随机信号和噪声都是随机过程。随机过程是一笼统的概念,平常指的是随机过程的任一实现。
2、通俗地说,随机过程是所有可能实现的所构成的总体。

3、一般来说,把一组随机变量定义为随机过程。在研究随机过程时人们透过表面的偶然性描述出必然的内在规律并以概率的形式来描述这些规律,从偶然中悟出必然正是这一学科的魅力所在。
4、随机过程是一连串随机事件动态关系的定量描述。随机过程论与其他数学、物理分支如位势论、微分方程、复变函数论、力学等有密切的联系,是在自然科学、工程科学及社会科学各领域研究随机现象的重要工具。
5、随机过程:是依赖于参数的一族随机变量的全体,参数通常是时间。
6、随机过程是一类随时间作随机变化的过程,具有变量过程和时间函数的过程。

如何理解随机过程的概念呢
随机过程(Stochastic Process)是一连串随机事件动态关系的定量描述。随机过程论与其他数学分支如位势论、微分方程、力学及复变函数论等有密切的联系,是在自然科学、工程科学及社会科学各领域研究随机现象的重要工具。
随机过程和扩散过程虽然都涉及动态变化,但它们在以下方面存在区别:概念定义:随机过程是一种描述时间上随机变化的数学模型,通常用于分析和预测实际系统中的随机事件。它强调的是时间维度上的变化和不确定性。
按有无平稳性分为:平稳随机过程和非平稳随机过程; 按有无各态历经分为:各态历经随机过程和非各态历经随机过程; 按功率谱特性分为:白色过程和有色过程,宽带过程和窄带过程。
随机过程和随机变量之间的区别和联系有哪些?
1、随机过程即在随机变量的基础上引入时间的概念,也可以简单理解为随机变量关于时间的函数。

2、随机过程与随机变量的不同之处是它比随机变量多一个时间变量。随机变量仅是试验结果的函数。
3、随机变量主要有两大类,一类是离散型,其统计规律用概率分布(分布律)来描述;另一类是连续型,其统计规律可用密度函数来描述 随机过程(Stochastic Process)是一连串随机事件动态关系的定量描述。
4、随 t 的不同取值,随机变量的数字特征是可以不同的,它的数学期望和方差是依赖于参数 t 的函数,我们称这一函数为随机过程的数字特征。
随机过程及应用
在概率论概念中,随机过程是随机变量的集合。若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。实际应用中,样本函数的一般定义在时间域或者空间域。
随机过程理论不仅涉及到日常生活,也涉及到了航空业。从随机过程的任何一个样本函数中,可以得到随机过程的所有统计信息。也就是说,任何样本函数的特征都能充分代表整个随机过程的特征。特征信息可以通过一次测量获得。
主要内容有随机变量、条件概率及条件期望、离散及连续马尔可夫链、指数分布、泊松过程、布朗运动及平稳过程、更新理论及排队论等;也包括了随机过程在物理、生物、运筹、网络、遗传、经济、保险、金融及可靠性中的应用。
随机过程一般用于option的定价,还有利率模型,具体比如Brownian Motion. SDE,鞅方法,Ito积分,Ito公式,F-K theorem,change of measure, risk neutral,girsanov定理什么的。
概率的概念常常应用在生活中,例如风险评估及以金融市场的交易等。政府也在环境法中应用概率,称为路径分析。例如中东冲突可能会对油价有某程度的影响,而油价对世界经济可能会有涟漪效应的影响。
包括预备知识、泊松过程、离散时间马尔可夫链、离散鞅、连续时间马尔可夫链、随机微分方程与宽平稳过程等8章。《应用随机过程》可供高等院校高年级学生与研究生作为教材使用,也可供教师及工程技术人员参考。
到此,以上就是小编对于随机过程简明教程的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏