本篇目录:
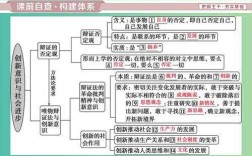
函数的形成与发展是什么?
函数的发展历程是:运算——解析式——变量的依赖关系或对应关系——映射——集合的对应关系——序偶集。11677年,格列高里:它是从其它的一些量经过一系列代数运算而得到的,或经过任何其他可以想象到的运算而得到。
”他的意思是凡变量x和常量构成的式子都叫做x的函数,并强调函数要用公式来表示。
引进了变量思想,并在他的《几何学》一书中指出:所谓变量是指不知的和未定的量,这成为数学发展的里程碑,也为函数概念的产生奠定了基础。
函数的起源﹙产生﹚十十七世纪,欧洲资本主义国家先后兴起,为了争夺霸权,迫切需要发展航海和军火工业。
历史 函数这个数学名词是莱布尼兹在1694年开始使用的,以描述曲线的一个相关量,如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数,数学家之外的普通人一般接触到的函数即属此类。
幂指函数的发展过程与前景
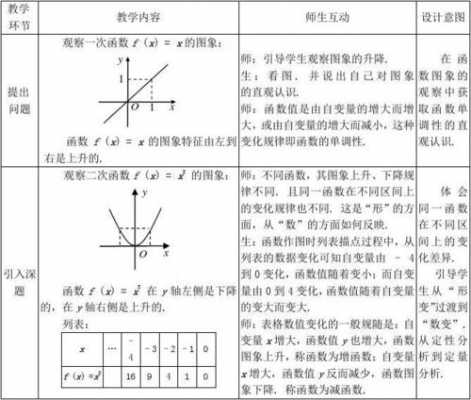
1、幂指函数既像幂函数,又像指数函数,二者的特点兼而有之。作为幂函数,其幂指数确定不变,而幂底数为自变量。相反地,指数函数却是底数确定不变,而指数为自变量。幂指函数就是幂底数和幂指数同时都含有自变量的函数。
2、年,刘人怀发展了Way的方法,提出修正幂级数法,求解了计及表层抗弯刚度的夹层圆板的大挠度方程。1944年,Bethe川用标量势函数近似方法求出了幂级数的首项,从而得到圆孔衍射场的远场解。
3、偶次根式被开方数≥0。零的零次方没有意义。对数真数0。最后求交集,写成集合或是区间。应用问题还看实际背景,比如整数,这也是常被遗忘的,比如出现2/3人这样的结果。
4、幂指函数就是幂底数和幂指数同时都为自变量的函数。这种函数的推广,就是广义幂指函数。首先要理解,函数是发生在集合之间的一种对应关系。然后,要理解发生在A、B之间的函数关系不止且不止一个。
周期函数的推导过程是什么?
周期(t)公式的推导可以基于正弦函数或余弦函数的性质来进行。我们以正弦函数为例进行推导。正弦函数是一个周期性函数,其定义为 f(x) = A * sin(ωx + φ),其中 A 是振幅,ω是角频率,φ是初相位。
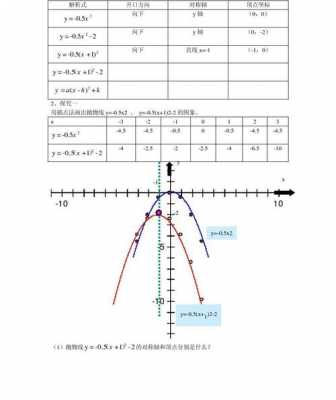
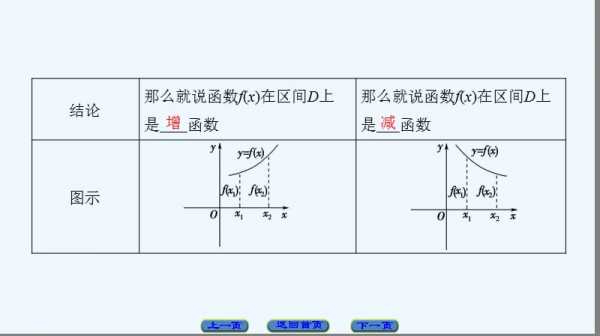
对于函数y=f(x),如果存在一个不为零的常数T,使得当x取定义域内的每一个值时,f(x+T)=f(x)都成立,那么就把函数y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期。
一般地,如果存在一个非零常数T,使得对于函数f(x)的定义域中的任意一个x和x+T,都有f(x+T)=f(x)。那么,函数f(x)就叫做周期函数,并且把非零常数T叫作这个函数的一个周期。
所以f(x)是以2a为周期的周期函数。f(x+a)=1/f(x)那么f(x+2a)=f[(x+a)+a]=1/f(x+a)=1/[1/f(x)]=f(x)所以f(x)是以2a为周期的周期函数。
到此,以上就是小编对于函数的形成过程怎么写的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏