本篇目录：

• 1、简单移动平均法简单移动平均法例题及解析
• 2、0阶截尾表示什么
• 3、用Excel做数据分析--移动平均
• 4、ARMA模型和ARIMA模型有什么区别?
• 5、数据分析技术:时间序列分析的AR/MA/ARMA/ARIMA模型体系
• 6、arima的自回归阶数和移动平均阶数怎么弄

简单移动平均法简单移动平均法例题及解析

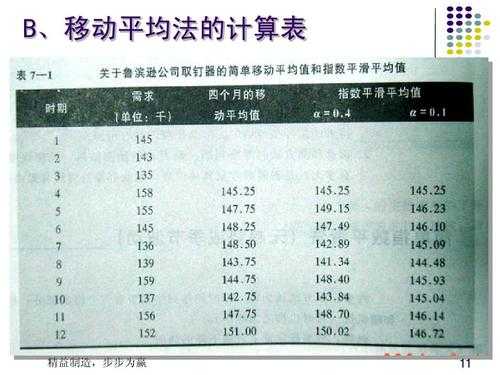
1、例：某企业 1 月～11 月份的销售收入时间序列如表 1 示。试用一次简单滑动平均法预测第 12 月份的销售收入。计算结果表明，N = 4 时，预测的标准误差较小，所以选取N = 4 。预测第12 月份的销售收入为996。

2、移动加权平均法例题及解析如下。移动加权平均法例题。

3、简单移动平均法（SimpleMovingAverage，SMA）是一种常见的技术分析方法，用于确定股票、期货、外汇等金融产品的趋势。SMA是一种统计方法，通过计算一定时间内的平均值来平滑价格波动。

0阶截尾表示什么

1、在计算机中表示成0001011101101110 其中第一个0是阶符表示指数是正的第九个0表示尾数是正的他们中间的就是阶码，后面的就是尾数。嗯就这样了，希望我讲清楚了，要是不明白可以继续问我。

2、截尾是指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后均为0的性质（比如AR的PACF）；拖尾是ACF或PACF并不在某阶后均为0的性质（比如AR的ACF）。

3、拖尾：如果样本自相关系数和样本偏自相关系数在最初的阶明显大于2倍标准差，而后百分之九十五的系数都落在2倍标准差的范围内，且非零系数衰减为小值波动的过程非常突然，通常视为k阶截尾。

4、有正弦波式的衰减；而所谓截尾是指从某阶后自相关或者偏相关系数为0.\x0d 判断标准：AR(P)自相关拖尾，偏相关p阶截尾MA(q)自相关q阶段截尾，偏相关拖尾\x0dAR(p)MA(q) 自相关q阶段截尾，偏相关p阶截尾。

用Excel做数据分析--移动平均

首先在Excel表格中输入几组数据，需要针对数据求平均值。点击空白单元格并选择“fx”插入函数中的“average”函数。

我们先计算了一下平均分，在平均分的那一栏输入函数：=AVERAGE(D2：D12)。

绘制简单移动平均可以使用Excel提供的数据分析工具。单击“数据”选项卡中的“数据分析”按钮，在打开的对话框中选择“移动平均”并单击“确定”按钮，将打开如图9-88所示的“移动平均”对话框。

ARMA模型和ARIMA模型有什么区别?

运用对象不同AR，MA，ARMA都是运用于原始数据是平稳的时间序列。ARIMA运用于原始数据差分后是平稳的时间序列。时间序列不同AR(自回归模型)，AR(p)，p阶的自回归模型。显然，ARMA模型描述的是一个时不变的线性系统。

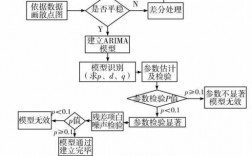
ARIMA（p，d，q）模型是ARMA（p，q）模型的扩展 ARMA谱估计 线性系统可以用线性差分方程进行描述，这种差分模型就是自回归---滑动平均模型（AutoRegression---Moving Average，ARMA ）。

很简单，不管是ARMA还是ARIMA模型，都是对平稳数据建模。前者是直接针对平稳数据建模，无需进行差分变换；后者则需要先对数据进行差分，差分平稳后再建模。

AR模型称为自回归模型（Auto Regressive model）；MA模型称为移动平均模型（Moving Average model）；ARMA称为自回归移动平均模型（Auto Regressive and Moving Average model）；ARIMA模型称为差分自回归移动平均模型。

AR，MA，ARMA都是运用于原始数据是平稳的时间序列。ARIMA运用于原始数据差分后是平稳的时间序列。时间序列不同AR(自回归模型)，AR(p)，p阶的自回归模型。MA(移动平均模型)，MA(q)，q阶的移动平均模型。

ARIMA（p，d，q）称为差分自回归移动平均模型，AR是自回归，p为自回归项，可以看自相关图来估计；MA为移动平均，q为移动平均项数，可以看偏相关图来估计，d为时间序列成为平稳时所做的差分次数。

数据分析技术:时间序列分析的AR/MA/ARMA/ARIMA模型体系

因为传统时间序列分析技术（时间序列分解法）的缺陷，所以统计学家开发出更为通用的时间序列分析方法，其中AR/MA/ARMA/ARIMA在这个发展过程中扮演了非常重要的角色，直到现在，它们都在实际工作生活中发挥重要作用。

ARIMA（p，d，q）称为差分自回归移动平均模型，AR是自回归，p为自回归项，可以看自相关图来估计；MA为移动平均，q为移动平均项数，可以看偏相关图来估计，d为时间序列成为平稳时所做的差分次数。

运用对象不同 AR，MA，ARMA都是运用于原始数据是平稳的时间序列。ARIMA运用于原始数据差分后是平稳的时间序列。时间序列不同 AR(自回归模型)，AR ( p) ，p阶的自回归模型。

arima的自回归阶数和移动平均阶数怎么弄

1、权重。例如 y (t) = 1/3 * y (t-3) + 1/3 * y (t-2) + 1/3 * y (t-1)， 又如 y (t) = 1/6 * y (t-3) + 4/6 * y (t-2) + 1/6 * y (t-1) 。

2、ARIMA 模型是用于时间序列预测的一种模型，其中 013 指的是模型的阶数，即自回归阶数（AR）、差分阶数（I）和移动平均阶数（MA）分别为 0、3。

3、ARIMA（p，d，q）中，AR是自回归，p为自回归项数；MA为滑动平均，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

4、确定 的方法有两种：一是利用样本偏自相关系数(pacf)； 另一种是利用信息注册函数方法。

5、MA表示移动*均模型（Moving Average）ARIMA模型记作ARIMA(p，d，q)，p为自回归项数；q为滑动*均项数，d为使之成为*稳序列所做的差分次数（阶数）。

到此，以上就是小编对于移动平均法怎么求的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。