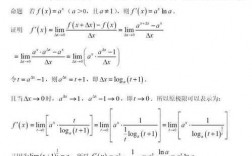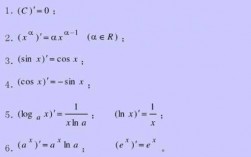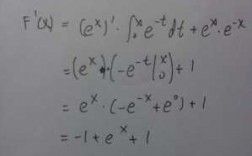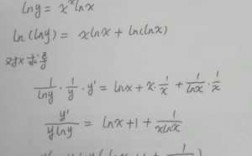本篇目录:
激活函数总结
1、该激活函数可以在移动端设备使用float16/int8低精度的时候也能良好工作。如果对 ReLU 的激活范围不加限制,激活值非常大,则低精度的float16/int8无法很好地精确描述如此大范围的数值,带来精度损失。缺点:与ReLU缺点类似。
2、当一个神经元以概率 keep_prob 为标准决定是否被激活,如果被激活,那么该神经元的输出将被放大到原来的 1/keep_prob 倍;如果不被激活,则神经元的输出为0。默认情况下,每个神经元是否被激活是相互独立的。
3、Rectified linear unit,x 大于 0 时,函数值为 x,导数恒为 1,这样在深层网络中使用 relu 激活函数就不会导致梯度消失和爆炸的问题,并且计算速度快。但是因为 x 小于 0 时函数值恒为0,会导致一些神经元无法激活。
梯度提升分类树原理推导(超级详细!)
梯度提升分类树的预测概率为 ,其中 表示决策回归树。但是由于梯度提升分类树的样本输出不是连续的而是离散的,因此无法直接拟合类别输出的误差。这时候需要构建交叉熵损失函数(也叫对数损失函数)。
GB代表的是Gradient Boosting,意为梯度提升,梯度是一种数学概念,一个函数的梯度方向是函数上升最快的方向,相反的,负梯度方向是函数下降最快的方向。
梯度提升树 由多个回归决策树 串联得到,因此建树时的分裂标准是均方误差和。梯度提升树的每个树都会拟合上棵树的拟合目标残差。

回归树算法如下图(截图来自《统计学习方法》1 CART生成): 梯度提升(Gradient boosting)是一种用于回归、分类和排序任务的机器学习技术 [1] ,属于Boosting算法族的一部分。
基于梯度提升算法的学习器 叫做 GBM(Gradient Boosting Machine)。理论上,GBM 可以选择各种不同的学习算法作为基学习器。GBDT 实际上是 GBM 的一种情况。
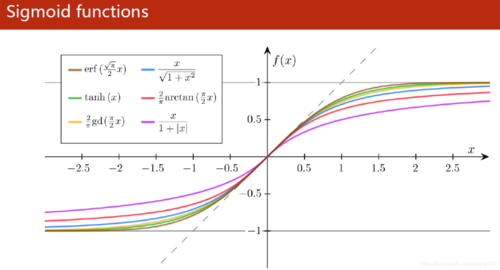
Sigmoid函数的求导证明
1、为什么要对Sigmoid函数求导?其实就是求极值。
2、常见的激活函数:sigmoid,tanh,relu。sigmoid是平滑(smoothened)的阶梯函数(step function),可导(differentiable)。sigmoid可以将任何值转换为0~1概率,用于二分类。细节可以 参考 。
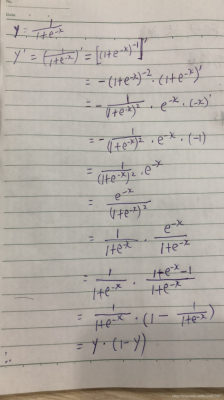
3、Sigmoid 和 ReLU 比较:sigmoid 的梯度消失问题,ReLU 的导数就不存在这样的问题,它的导数表达式如下:曲线如图 对比sigmoid类函数主要变化是: 1)单侧抑制 2)相对宽阔的兴奋边界 3)稀疏激活性。
4、求 对于 的一阶导数: 令 ,有 利用sigmoid函数求导公式,求 对于 的二阶导数: 以上就是单个样本的损失函数推导,那么整体的损失函数也就容易了,就是单个样本的累加。
5、常见的激励函数:sigmoid函数、tanh函数、ReLu函数、SoftMax函数等等。
到此,以上就是小编对于sigmoid函数求导的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏