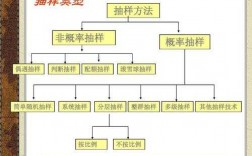
本篇目录：

• 1、数学期望和方差公式怎么推导的?
• 2、方差的公式怎么推导?
• 3、超几何分布的期望和方差公式推导。?
• 4、如何推倒样本均值期望和方差公式?
• 5、几何分布的期望与方差公式怎么推导
• 6、几何分布的期望和方差公式推导

数学期望和方差公式怎么推导的?

Y~N（2，3/4）数学期望E（Y）＝2，方差D（Y）＝4/3。

你好！根据性质，它们和的方差等于各变数方差之和，每个几何分布的方差是(1-p)/p^2，所以总的方差是n(1-p)/p^2。经济数学团队帮你解请及时采纳。

二项分布的期望和方差公式推导如下：二项分布求期望：公式：如果r～ B(r，p），那么E(r)=np。示例：沿用上述猜小球在哪个箱子的例子，求猜对这四道题目的期望。

期望值计算公式：E(X)=(n*M)/N [其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

正态分布的期望用数学符号表示ξ，所以正态分布的期望的公式是：Eξ=x1p1+x2p2+……+xnpn。而方差用数学符号表示s，所以正态分布的方差的公式是：s=1/n[(x1-x)+(x2-x)+……+(xn-x)]，另外x上有“-”。

期望的公式：E=X1*P1+X2*P2+X3*P3+.+Xn*Pn。高中数学期望与方差公式应用：1）随机炒股。

方差的公式怎么推导?

1、方差=E(x)-E(x)，E(X)是数学期望。在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

2、推导另一种计算公式得到：“方差等于各个数据与其算术平均数的离差平方和的平均数”。其中，分别为离散型和连续型计算公式。

3、根据方差的性质，有D(X+Y)=DX+DY，以及D(kX)=k^2*DX，其中X和Y相互独立，k为常数。

超几何分布的期望和方差公式推导。?

1、超几何分布的期望和方差公式：E(X)=(n*M)/N[其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

2、超几何分布的期望值计算公式为Ex=nM/N，其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数，超几何分布的方差计算公式为Vx=Xn_Pn-a_，其中a为期望值。

3、超几何分布的期望和方差是EX=nM/N，超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回）。

4、方差公式是V(X)=X1^2*P1+X2^2*P2+...Xn^2*Pn-a^2[这里设a为期望值]。超几何分布是统计学上一种离散概率分布。

5、超几何分布期望值的简单公式法，E(X)=(n*M)/N，［其中x是指定样品数，n为样品容量，M为指定样品总数，N为总体中的个体总数］，可以直接求出均值。

如何推倒样本均值期望和方差公式?

样本均值期望和样本均值方差推导：E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。

有n个数，先求平均值Ex，则方差var(n)=/n。“方差”（variance）这一词语率先由罗纳德·费雪（Ronald Fisher）在其论文《The Correlation Between Relatives on the Supposition of Mendelian Inheritance》中提出。

期望值计算公式：E(X)=(n*M)/N [其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

几何分布的期望与方差公式怎么推导

1、你好！根据性质，它们和的方差等于各变数方差之和，每个几何分布的方差是(1-p)/p^2，所以总的方差是n(1-p)/p^2。经济数学团队帮你解请及时采纳。

2、超几何分布的期望和方差公式：E(X)=(n*M)/N[其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

3、几何分布，P(X=n)=(1p)^(n1)p，随着n增大呈等比级数变化，等比级数又称几何级数。这可能和以前几何学中无限分割图形得到的级数有关。

几何分布的期望和方差公式推导

你好！根据性质，它们和的方差等于各变数方差之和，每个几何分布的方差是(1-p)/p^2，所以总的方差是n(1-p)/p^2。经济数学团队帮你解请及时采纳。

超几何分布的期望和方差公式：E(X)=(n*M)/N[其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

几何分布的期望和方差公式分别是E(n)等于1/p、E(m)等于(1-p)/p，几何分布是离散型概率分布。其中一种定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。

高中数学教科书新版第三册（选修II）比原来的修订本新增加随机变量的几何分布，但书中只给出了结论：（1）（2），而未加以证明。几何分布的期望与方差计算要用到级数求和，过程如图。

超几何分布期望值的简单公式法，E(X)=(n*M)/N，［其中x是指定样品数，n为样品容量，M为指定样品总数，N为总体中的个体总数］，可以直接求出均值。

到此，以上就是小编对于期望与方差公式推导的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。